I'm doing some PCA on scaled features but where I also have some binary variables.
When I include the binary features they seem to really impact the PCA and I'm concerned that they will also disproportionately impact the cluster analysis I'm planning to do with kmeans too.
library(tidyverse)
library(factoextra)
df <- diamonds %>% select(depth:z) %>%
lapply(function(x) {(x - min(x)) / (max(x) - min(x))}) %>% as.data.frame()
df$cut = diamonds$cut
df_small <- df %>% sample_n(1000)
clust_fact <- df_small$cut %>% factor()
df_small <- df_small %>% select(-cut)
df.pc <- princomp(df_small)
pc1_cont <- fviz_contrib(df.pc, choice = "var", axes = 1)
When you then enter pc1_cont into the console you see:
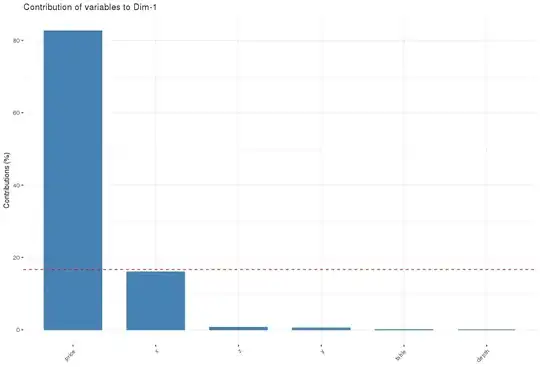
This is the contribution of each feature to PC1. You can see that price shows the most impact to PC1.
Now, if I add a binary feature, look what happens:
df <- diamonds %>% select(depth:z) %>%
mutate(carat_binary = if_else(diamonds$carat >= 0.8, 1, 0)) %>% # add binary feature
lapply(function(x) {(x - min(x)) / (max(x) - min(x))}) %>% as.data.frame() # scale between 0 and 1
df$cut = diamonds$cut
df_small <- df %>% sample_n(1000)
clust_fact <- df_small$cut %>% factor()
df_small <- df_small %>% select(-cut)
df.pc <- princomp(df_small)
pc1_cont <- fviz_contrib(df.pc, choice = "var", axes = 1)
The new binary feature is shown to have the largest impact. This echos what I've found on my own actual data, each time I include a binary it shows as having the most impact.
I found some posts on here for handling this but struggled to understand the guidance. I was pointed to academic papers.
Is there a conventional approach to 'taking the edge off' binary features in PCA and clustering? In my mind it makes sense that they distort things since they will always be at the extreme of the sale of the entire data set, 0 or 1.
I was thinking of doing something crude like just transforming the true case as being the mean of across all scaled numeric variables in my data frame and then the false case as perhaps the 1st quartile value. But I'm thinking of arbitrary solutions here.
Is there a straight forwards approach in r for dealing with this?