My research question is assessing if a variable (let’s call it ‘x') can predict another variable (let’s call it ‘y’). The two variables x and y are in the same units, but they just come from different sources of information. I have data on x and y for some 30 different populations in which values of x and y vary by as much as two orders of magnitude (simply because the populations are different; the data are believed to be as accurate as possible). For each population, values of x are generally close to y, suggesting that x can predict y. But, for each population, values of x show some variability, and values of y are often near-constant. X values show variability because they are individual-level observations and y values show little or no-variability because they are population averages. Unfortunately, for this research, it is impossible to obtain individual-level bservations of y, so I have no choice but to compare the two sets of variables.
In trying to address my research question, I have been using regression methods. This is what I have found so far:
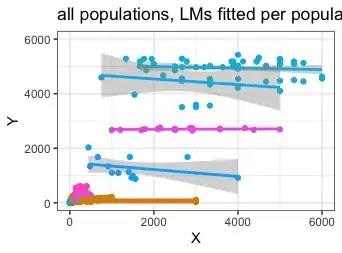
- When I do a simple linear regression for each population (separately) of y ~ x , I get that R2 is often near-zero, because y varies little. According to this post $R^2$ of linear regression with no variation in the response variable, this situation is one in which R2 is undefined. Note that this would still be the case even if x values did perfect predictions of y. See one example of my preliminary LM results for one such population below.
Call: lm(formula = y_pop1 ~ x_pop1, data = df_pop1)
Residuals:
Min 1Q Median 3Q Max
-958.9 -674.2 -68.8 550.9 1091.7
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 4745.9153 488.7394 9.711 1.34e-07 ***
x. -0.1039 0.1615 -0.643 0.53
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 703.7 on 14 degrees of freedom
Multiple R-squared: 0.02872, Adjusted R-squared: -0.04066
F-statistic: 0.4139 on 1 and 14 DF, p-value: 0.5304
- When I do a simple linear regression of y ~ x for all populations together, without accounting for each population (i.e., as a random effect), I get that R2 is high (~ 0.77). In this case, the relationship is due to the large difference in x and y values across all populations and the (somewhat) close agreement of x and y values within populations; these produce a (near) linear relationship, with increasing y values being followed by increasing x values. See preliminary LM results below. I cannot analyze my data this way, because I have different populations and need to account for differences among them. Such an analysis, I understand, would be subject to Simpson's Paradox (https://en.wikipedia.org/wiki/Simpson%27s_paradox).
Call:
lm(formula = y ~ x, data = df)
Residuals:
Min 1Q Median 3Q Max
-6110.1 -126.4 -105.3 -63.5 4061.0
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 118.43118 26.21227 4.518 7.18e-06 ***
x. 0.82621 0.01565 52.780 < 2e-16 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 685.5 on 800 degrees of freedom
Multiple R-squared: 0.7769, Adjusted R-squared: 0.7766
F-statistic: 2786 on 1 and 800 DF, p-value: < 2.2e-16
- I have thus been trying to analyze my data using linear mixed models (LMM), where x predicts y and each population is a random effect. I am far from a statistician (or someone with strong understanding of statistics), but my understanding is that a LMM such as this one would assess if y can be predicted by x, while accounting for differences among populations. In other words, I believe this is the “right” approach for my analysis. Some preliminary LMM results are below, indicating that x does indeed predict y, though there is a tendency to under-estimate. Variable values for this LMM have been standardized (but the results are same when they are not standardized).
Linear mixed model fit by maximum likelihood ['lmerMod']
Formula: y ~ x + (x - 1 | population)
Data: datall
AIC BIC logLik deviance df.resid
998.3 1017.1 -495.2 990.3 798
Scaled residuals:
Min 1Q Median 3Q Max
-8.2535 -0.1715 -0.0452 0.0185 5.5351
Random effects:
Groups Name Variance Std.Dev.
Population x 0.1453 0.3812
Residual 0.1906 0.4366
Number of obs: 802, groups: f.name, 33
Fixed effects:
Estimate Std. Error t value
(Intercept) 0.20933 0.03785 5.53
x. 1.39751 0.11417 12.24
Correlation of Fixed Effects:
(Intr)
x. 0.651
R2m R2c
0.8532974 0.9167095
My question is whether the LMM above is producing misleading results given my points in 1 and 2. I would like to confirm that the LMM is indeed able to find relationships between x and y when considering and accounting for data for all populations together, even though LMs for each population separately cannot. IF there is a problem with such an analytical approach, I would be very interested in hearing alternative approaches to analyzing this data. I have not identified any so far.
Many thanks!