I'm working with a model where we are studying a marker for a disease as well as risk factors, demographic variables, and related conditions.
Marker: Marker concentration (continuous)
Age: continuous
Case/Control: Disease State
Gender: M/F
ARMS2rs10490924: genetic risk factor
CFHrs1061170: genetic risk factor
CFHrs10737680: genetic risk factor
SKIV2Lrs429608: genetic risk factor
CNV_Either_Eye: related disease---possible precursor
GA_No_CNV_Either_Eye: related disease---possible precursor
AREDS: Treatment that works, but may affect marker concentration
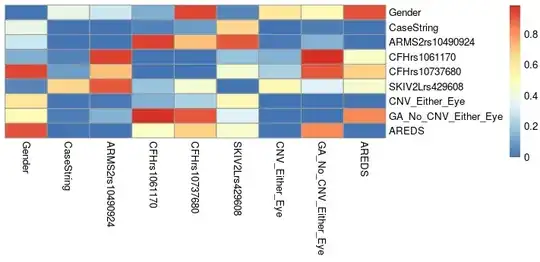
Many of the categorical variables are highly correlated.
Here is a heatmap of the p-values from $\chi^2$ tests between pairs of variables:
Additionally, the AREDS variable is correlated with age because it is an age-related disease and very few control subjects are using the treatment (prophylactically) while almost all of the disease subjects are.
I want to perform a linear regression such as:
lm(MarkerConcentration ~ Case + Age + ... <categorical variables> ...)
What should be my strategy to deal with the colinearity between my variables?
EDIT: Here is a typical VIF:
> fit = lm(Shannon ~ CaseString + Age + Gender + ARMS2rs10490924 + CFHrs1061170 + CFHrs10737680 + SKIV2Lrs429608 + CNV_Either_Eye + GA_No_CNV_Either_Eye + AREDS, data=all_master_table)
> vif(fit)
GVIF Df GVIF^(1/(2*Df))
CaseString 6.774346 1 2.602757
Age 1.356645 1 1.164751
Gender 1.215620 1 1.102552
ARMS2rs10490924 1.397811 2 1.087332
CFHrs1061170 3.489505 2 1.366756
CFHrs10737680 3.390033 2 1.356910
SKIV2Lrs429608 1.268326 2 1.061226
CNV_Either_Eye 5.174471 1 2.274746
GA_No_CNV_Either_Eye 2.740709 1 1.655509
AREDS 2.325022 1 1.524802