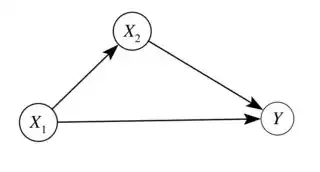
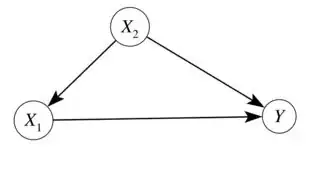
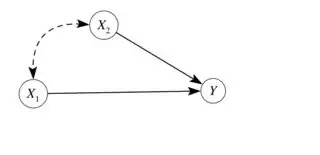
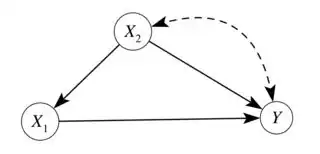
I know that in general a structural causal model (SCM) can be written in terms of structural equations. And in a more qualitative but formal manner, we can rewrite a structural model in terms of DAG.
Now suppose we have a simple structural equation like this:
$$y = \beta_0 + \beta_1x_1 + \beta_2 x_2 + .. + \beta_n x_n + e$$
where $e$ is completly exogenous. We don't know anything else about the model.
How can we write this model in a DAG?
EDIT Moreover I have some sub-questions:
1) the SCM above imply that $E[y|do(x_1,...,x_n)] = \beta_0 + \beta_1x_1 + .. + \beta_n x_n$ , now is true that $E[y|do(x_1,...,x_n)] = E[y|x_1,...,x_n]$ regardless the causal nexus among $x$s?
2) if we known only a subsample of dependent/causal variables like $x_1,...x_k$ with $k<n$ then we have a problem that sound like omitted variables. Now exist a way for find the others variables ($x_{k+1},...,x_n$)?
2a)If it exist, the causal nexus among $x$s become relevant?
2b)If it not exist, is still possible to identify the causal parameters $\beta_1,...,\beta_k$?