2

I read in a textbook (Japanese one) that the spherical covariance function is only valid for dimensions $d = 1,$ $2,$ and $3.$ I have the following questions:

  1. Does that mean the spherical covariance function is not positive definite for $d\gt 3?$
  2. Is there any material which contains a proof of (1)?
whuber
  • 281,159
  • 54
  • 637
  • 1,101
Jiro
  • 23
  • 3

1 Answers1

4

There are at least two conventional meanings of "spherical covariance function." Based on the conclusion you want to draw, we can infer you are referring to the family of functions $G:\mathbb{R}^n\to \mathbb{R}$ based on

$$G(\mathbf{h}) = 1 - \frac{3|\mathbf{h}|}{2} + \frac{|\mathbf{h}|^3}{2},\ 0 \le |\mathbf{h}| \le 1,$$

and otherwise $G=0.$ ("Based on" means we can ignore scale factors in both $\mathbf h$ and $G$ without any loss of generality merely by choosing our units of measurement appropriately.)

A positive-(semi)definite covariance $C$ is one that satisfies

$$\sum_{j,k} a_j C(\mathbf{y}_j - \mathbf{y}_k) \bar{a_k} \ge 0$$

for any collection of locations $\mathbf{y}_i \in \mathbb{R}^n, i=1,2,\ldots, m$ and all possible complex numbers $(a_i), i=1,2,\ldots, m.$ In other words, the covariance matrix associated with any set of locations is positive-semidefinite.

Bochner's Theorem asserts that all positive-definite covariances arise as the Fourier transforms of finite positive measures $F$ given by

$$\hat F(\mathbf{h}) = \int_{\mathbb{R}^n} e^{i\mathbf{h}\cdot \mathbf{x}} F(\mathrm{d}\mathbf{x}).$$

Indeed, by interchanging summation and integration we may check that

$$\eqalign{ \sum_{j,k} a_j C(\mathbf{y}_j - \mathbf{y}_k) \bar{a_k} &= \sum_{j,k}\int_{\mathbf{R}^n}a_j e^{i(\mathbf{y}_j - \mathbf{y}_k)\cdot \mathbf{x}} \bar{a}_kF(\mathrm{d}\mathbf{x}) \\ &= \int_{\mathbf{R}^n} \sum_j a_j e^{i\mathbf{y}_j\cdot \mathbf{x}}\ \sum_k \overline{e^{i\mathbf{y}_k \cdot\mathbf{x}}a_k}\ F(\mathrm{d}\mathbf{x}) \\ &= \int_{\mathbf{R}^n} \left|\sum_j a_j e^{i\mathbf{y}_j\cdot \mathbf{x}}\ \right|^2\ F(\mathrm{d}\mathbf{x}) \ge 0. }$$

Because (for spherical covariances) the expression $ C(\mathbf{y}_j - \mathbf{y}_k) $ depends only on the separation distances $r_{jk}=|\mathbf h_{jk}| = |\mathbf{y}_j - \mathbf{y}_k|,$ the Fourier transform can be inverted (to find $F$ from $G$) with a single integration. By doing the calculation we find the following measures $F(\mathrm{d}\mathbf{x}) = F(r)\mathrm{d}r \mathrm{d}\Omega$ in spherical coordinates $(r, \Omega)$ for $n=3,4:$

$$n=3:\ F(r) \propto r^{-6}\left(r \cos(r/2) - 2 \sin(r/2)\right)^2 \ge 0.$$

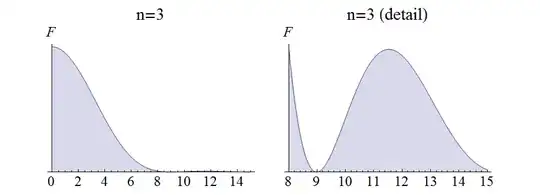
Figure plotting spectral density for n=3

$$n=4:\ F(r) \propto r^{-6}\left(\left(r^2+5\right) (\pmb{H}_0(r) J_1(r)-\pmb{H}_1(r) J_0(r))+30 r (r J_0(r)-3 J_1(r))\right),$$

an algebraic combination of Bessel J functions $J_i$ and Struve H functions $\pmb{H}_i.$

Figure plotting spectral density for n=4

Because some of the possible values of this density are negative, the spherical covariance function for $n=4$ is not positive-definite.

We are actually done: we don't have to consider all possible dimensions. The reason is that some configurations of points in $\mathbb{R}^n$ actually lie within lower-dimensional subspaces. Consequently, it is immediate from the definition of positive-definite functions that

  1. When a covariance in $\mathbb{R}^n$ is positive-definite, it remains positive-definite in all lower dimensions.

  2. When a covariance in $\mathbb{R}^n$ fails to be positive-definite, it fails in all higher dimensions.

Reference

This post broadly follows the exposition in a set of Duke University lecture notes (unattributed and undated) found at https://www2.stat.duke.edu/courses/Fall01/sta293/lecs/covar.pdf. Its bibliography covers the classics: Yaglom, Matern, Ripley, Cressie.

Community
  • 1
whuber
  • 281,159
  • 54
  • 637
  • 1,101
  • Which book should I read to understand the derivation of (1) or (4) from the first line in the lecture notes? §1.1 is too brief for me. – Jiro Jul 22 '19 at 07:08
  • The reference to "Watson 1944" is almost surely the second edition of Watson's *Treatise on the Theory of Bessel Functions,* available online at https://ia802601.us.archive.org/30/items/ATreatiseOnTheTheoryOfBesselFunctions/Watson-ATreatiseOnTheTheoryOfBesselFunctions.pdf. For an easier introduction see Whittaker and Watson, *A Course of Modern Analysis* (1927 edition, Cambridge U. Press). – whuber Jul 22 '19 at 19:59
  • Thank you for letting me know about those books. But I can't follow changes of variables before the line involving a Bessel function. In §1.1, I see that $d^nx = \frac{2\pi^{n/2}}{\Gamma(n/2)}r^{n-1}dr\,d\sigma$ and $∑_{j=1}^n σ_j^2 = 1$, but the last sentence of that section doesn't make sense to me at all. (I know very basic definitions and properties of Bernoulli and Dirichlet distributions.) – Jiro Jul 23 '19 at 05:50
  • I take "$\sigma_j$" to be coordinate $j$ on the unit sphere $S^{n-1}\subset\mathbb{R}^n.$ For the uniform distribution on $S^n,$ $(\sigma_j+1)/2$ has a Beta$((n-1)/2,(n-1)/2)$ distribution: https://stats.stackexchange.com/a/85977/919. The claim in the paper is correct only if $\sigma_j$ is taken to be the *absolute value* of the coordinate. In that case the $\sigma_j^2$ have the same distribution as $x_j^2/(x_1^2+\cdots+x_n^2)$ for iid standard normal variables $x_i,$ which is easily seen to be a Gamma$(1/2)$ distribution, whence $(\sigma_j)^2$ has a Dirichlet$(1/2,\ldots,1/2)$ distribution. – whuber Jul 23 '19 at 14:51
  • Finally, simply by integrating out $\sigma_2,\ldots,\sigma_n,$ you find that the marginal distribution--that of any $\sigma_j^2$--is Beta$(1/2,(n-1)/2)$: see https://en.wikipedia.org/wiki/Dirichlet_distribution#Marginal_distributions. – whuber Jul 23 '19 at 14:53
  • 1
    Thank you very much! Now I understand that $u \in [0, 1]$ is defined as $u = \sigma_h^2$ and its distribution is $\mathrm{Beta} (\frac{1}{2}, \frac{n-1}{2})$. – Jiro Jul 25 '19 at 08:20