Is it valid to use t-test when using ratio of two variants

Question

Consider a setup where it is not possible to show different variants to different users. But we still would like to measure the performance of different variants. We would like to use the following approach:

• Find two similar performing websites. Let's call them control and test.
• Add changes to the test site (the changes we want to test)
• Use the ratio of the two websites to investigate the impact of the changes
• Calculate the significance by using the ratio before the test and during the test.

Different metrics could be considered but we can assume number of conversion for this example.

Here an example in python (jupyter notebook):

import numpy as np
import pandas as pd
import math
%matplotlib inline
import matplotlib.pyplot as plt
from scipy import stats

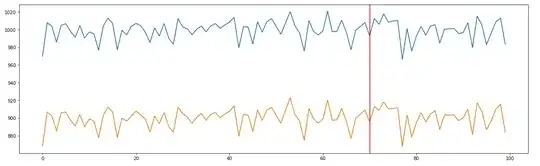
Two example websites (control and test). These two websites would be considered for the test as they have similar performance. The changes on the test website are added after epoch 70. The last 30 data points are considered the testing phase.

base = np.random.randn(100)*10
control = [1000 for _ in range(100)] + base
test = [900 for _ in range(70)] + [902 for _ in range(30)] + np.random.randn(100) + base

Let's plot the performance of the two websites. The red vertical line indicates the start of the test phase.

plt.figure(figsize=(20, 6))
plt.plot(a)
plt.plot(test)
plt.axvline(x=70, c='r')

Let's calculate and plot the ratio:

ratio = control / test
plt.figure(figsize=(20, 6))
plt.plot(ratio, 'y--')
plt.show()

Calculate the significance:

def ttest(a, b):
    tstat, p_ttest = stats.ttest_ind(a, b)
    k2, p_norm = stats.normaltest(a)
    if p_norm >= 1e-3 :
        print(f"normally distributed p={p_norm}")
    else:
        print(f"not normally distributed p={p_norm}")
    if p_ttest > 0.05 :
        print(f"ttest difference not significant p={p_ttest}")
    else:
        print(f"ttest difference significant p={p_ttest}")

ttest(ratio[:70], ratio[70:])

Result:

normally distributed p=0.783668458064106
ttest difference significant p=2.1238045469602226e-11

Is this a valid approach?

Is it valid to use a t-test in such a setup?