I'm creating a generalised linear regression using a binomial link function for two variables A and B. From looking at the data it appears that A/B may have discriminatory effect. Is it sensible to include A/B as an additional term in the model? Thinking about this myself, this appear term would be the inverse of including the interaction term A:B and therefore not the same as including the interaction.
EDIT 1:
Having thought about this a little bit more, if I include variables on a log scale would this be the same as including a ratio when the parameter estimates are negative?
EDIT 2:
I am experimenting with machine learning and have been exploring example data
sets in the R package. I am currently using the data(crabs) in the MASS
package and trying to predict crab gender and species from morphological
variables. I first looked at the PCA of the variables to identify underlying
vectors within the data. The first component in the PCA is all positive with
respect to each variable, and from my understanding of PCA this means the
variables are all correlated along this component. The second component
contains both positive and negative values, specifically carapace width and
rear width. A dot plot and density plot of these variable indicates two
possible distributions.
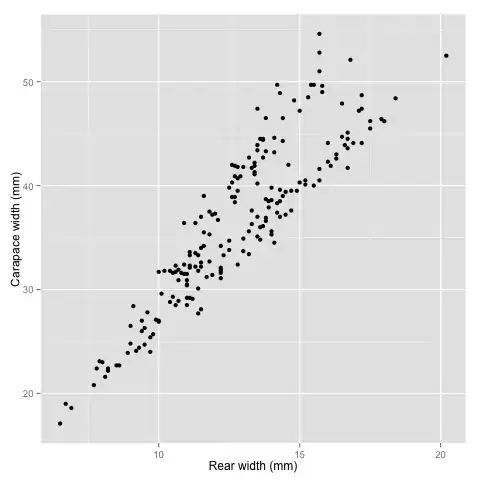
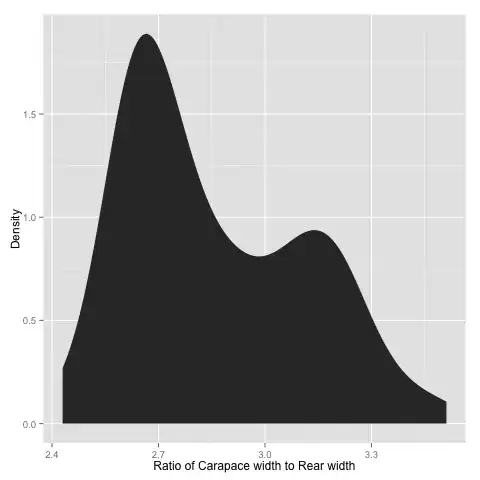
Is it therefore sensible to use the following logistic model for predicting species:
species ~ CW + RW + I(CW/RW)
As Stuart mentioned in the comments, these variables may be correlated with each other and therefore non-independent. I used bootstrapping of the crab data to test the models' accuracy. For the case of predicting sex, including the ratio term does seem to improve the model's predictive accuracy slightly.
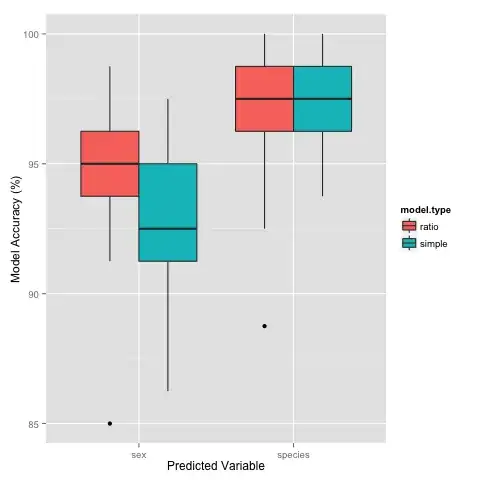
I should also note that including all available measured variables improves the model accuracy but I would like to try and "infer" what the important variables may be using PCA.