In the logisitic regression chapter of "Data Analysis Using Regression and Multilevel/Hierarchical Models" by Gelman and Hill, The "Divide by 4" rule is presented to approximate average marginal effects.
Essentially, dividing the estimated log-odds ratio gives the maximum slope (or the maximum change in probabilities) of the logistic function.
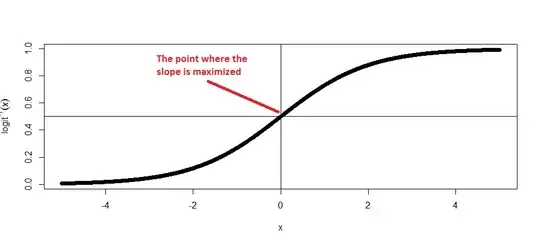
Since the text above states that the "divide by 4 rule" gives the maximum change in $P(y=1)$ with a unit change in x, why is the estimated 8% less than the 13% calculated from actually taking the derivative of the logistic function in the example given?
Does the "divide by 4 rule" actually give the upper bound marginal effect?
Other "divide by 4" resources: