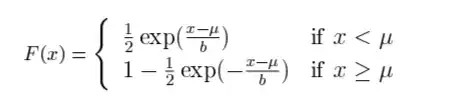I have done a logistic regression with two independent variables (x1 and x2) and a dependent binary variable (y). The AUC (roc curve) is 0.7915.
The heatmap below shows the probabilities resulting from the predict function. It seems the logistic regression is not flexible enough since the range of p (probabilities) for x1=10 is 0.25 – 0.76 while in reality this range is 0.25 – 1.
For that reason I have use the GAM - package to create a GAM with smoothing splines.
mygam=gam(y~s(x1,df=100)+s(x2,df=100),family=binomial,data=mydata3)
This generates an improvement in AUC to 0.807. The heatmap below shows the probabilities resulting from the GAM-predict function.
Although there is still an area for x1 between 0 and 10 where the GAM shows large differences in comparison to a Pivot-table of my raw data (for every (x1,x2): count(y==1) / total y). The heatmap below shows the differences between the GAM and the Pivot table:
Even if I set the degrees of freedom higher than 100, this give no improvement. I have also tried lo for local regression although no improvement. I also have tried several settings with mgcv although it seems not possible to make a GAM flexible enough to fit the range for x2 between 0 and 10.
Would there be any possibility to reach the fit with a GAM or is the data to steep?
Thanks a lot!
Ps: only the labels in the first graph are swapped (not the variables).