0

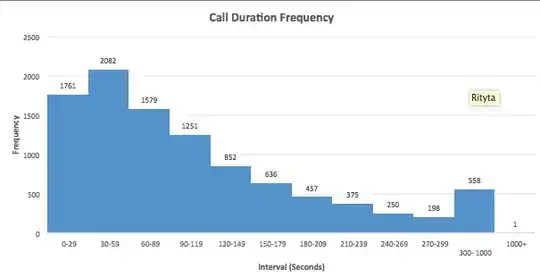
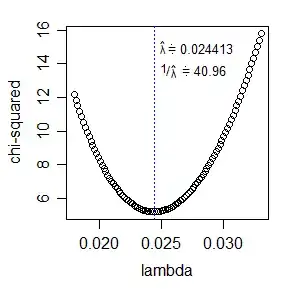
I am working on a time series with around 2500 data points. I have used the ADF test to check for the stationarity of the series, the series passed the test and results are shown below enter image description here

But when I perform ACF and PACF test, there is slow decay of ACF (shown below) which means my time series is non-stationary. So do I have to difference the time series at this point to make it stationary?

enter image description here

raginibm
  • 1
  • 2
    In what sense did your data "pass the test"? The output in the first image appears to show very strong evidence of non-stationarity. – whuber Jun 13 '19 at 16:59

2 Answers2

1

Well, I am not 100% sure of what I am about to say, but I don't see why a slow decay in ACF implies non-stationarity, for example:

Let $x_t:= 0.999*x_{t-1} + \epsilon_t$ where $\epsilon_t$ follows a $N(0,1)$ distribution for every $t$ and $\{\epsilon_t\}$ presents no autocorrelations

$\{x_t\}$ is therefore a stationary series that will present high positive autocorrelations for a lot of lag values. It will eventually converge to $0$, but $\rho_{1000} = 0.9999^{1000}$ is still $0.9$

David
  • 2,422
  • 1
  • 4
  • 15
  • So what 'q' value could be used for the ARMA(4,q) model considering the delayed convergence? – raginibm Jun 13 '19 at 19:05
  • Well, it's complicated. Sometimes it's more of an art than a science. My approach would be to stay with the simplest valid model. One of the ways to check if a model is valid is taking the residual series and checking for its ACF/PACF. Ideally, they should show no autocorrelation – David Jun 13 '19 at 21:42
  • When people say a "slow decay" in ACF implies non-stationarity, they mean "slower than exponential". It would be hard to tell the difference using the ACF estimated at the first 25 lags if the lag-1 autocorrelation were as high as 0.9999; but here it's only about 0.9, & should have decayed much quicker than this if the serieswere stationary. – Scortchi - Reinstate Monica Jun 14 '19 at 09:17
  • @Scortchi That is true for a lag-1 process like an ARIMA(1,0,1), but there is no guarantee of that being the case. Real-life data often follows much complicated patterns – David Jun 14 '19 at 09:30
  • All stationary ARMA($p,q$) models exhibit exponential decay (sometimes with sinusoidal oscillations) in either the ACF or PACF for lags after $\max(p,q)$. Anyway, if you've a stationary ARMA model you think would fit the patterns in the ACF & PACF of this series, why not describe it in your answer? – Scortchi - Reinstate Monica Jun 14 '19 at 13:04
0

See The difference between the three Augmented Dickey–Fuller test (none,drift, trend). Note that you're effectively performing a test of the hypothesis the de-trended series has a unit root ("Exogenous: Constant, Linear Trend"). A de-trended series with no unit root is quite consistent with the empirical auto-correlation functions you show if the deterministic linear trend is strong.

Scortchi - Reinstate Monica
  • 27,560
  • 8
  • 81
  • 248