0

The software I'm using for this task is R. I am looking at three things :

  1. How one continuous variable is affected by three categorical variables, two with two levels one with four levels.

  2. Which level in each category affects the continuous variable the most.

  3. The individual "weight" and significance of each category in predicting the continuous variable, and the interactions between them. For example, do category 1 level 2 and category 3 level 4 have a significant effect on the continuous variable more than category 1 level 2 and category 3 level 1?

I know I should use either a GLM or a LM, but I cannot work out which - I have run both in R and come up with different results, which apparently shouldn't happen.

A brief overview of the correct model output would be greatly appreciated.

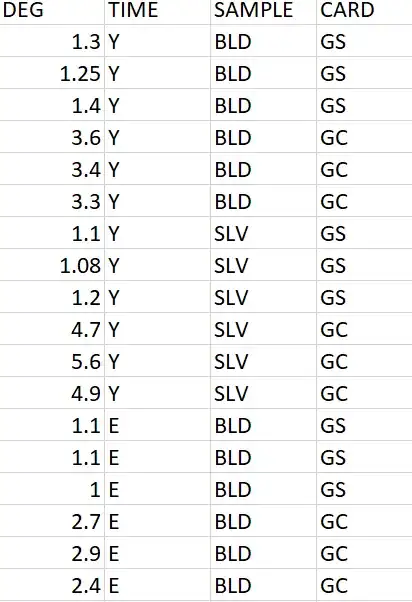
my data looks like this

continuious varaible DEG Time (year, eight, two,day) sample (BLD, SLV) Card (GS, GC)

e.g.: enter image description here

This is my code for both:

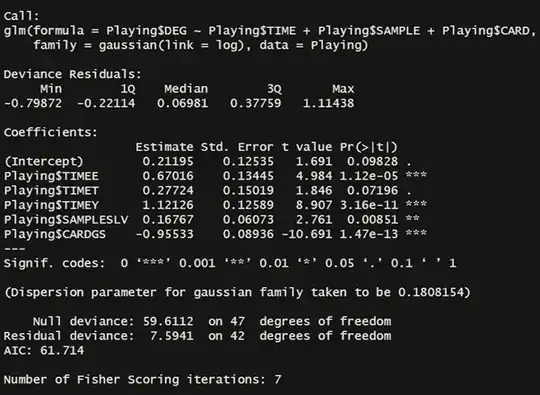
glm(Playing$DEG ~ Playing$TIME + Playing$SAMPLE + Playing$CARD,family = gaussian(link = log), data = Playing)

lm(Playing$DEG ~ Playing$TIME + Playing$SAMPLE + Playing$CARD,data = Playing)

I have already converted the predictors to factors.

My main issue is according to the research I have done both my GLM and LM models should give the same (or close enough) results - for some reason this isn't happening in R I cannot see an error in my code thus I must have misunderstood something along the way therefore which results do I use - GLM or LM model ? and how does this give me the interactions between/weight of the factors ?

Thanks for putting up with this confused new user !

(These are the results I am getting by the way - enter image description here enter image description here

TiredKaz
  • 1
  • 4
  • I have seen that post however I am still unsure how to know which to use specifically for my data - do I use GLM or LM ? futhermore if I have understood that post correctly I should be getting similar or same results for both models and I am not – TiredKaz Jun 06 '19 at 14:06
  • 1
    Welcome to Cross Validated! The highest-voted [answer](https://stats.stackexchange.com/a/181180/17230) describes exactly the cases you've given in your question & explains how the models are different. If you've a question specifically on how best to model your data, you'll need to edit your question to provide some information about them. See also posts tagged with [importance](https://stats.stackexchange.com/search?tab=votes&q=%5bimportance%5d%20is%3aquestion). – Scortchi - Reinstate Monica Jun 06 '19 at 14:15
  • Thank you - Ah ... I am clearly misunderstanding that post then - will update question – TiredKaz Jun 06 '19 at 14:19
  • 1
    `lm` does not use a log link: it is tantamount to using an *identity* link in `glm`. Please read the help page for `family` for more information. – whuber Jun 06 '19 at 15:08
  • Ok right I understand why they are different now (Thank you very much) - So which would be better for my analysis ? – TiredKaz Jun 06 '19 at 15:15
  • See [GLM: verifying a choice of distribution and link function](https://stats.stackexchange.com/q/141181/17230). Note that the dispersion parameter for a Gaussian family generalized linear model is the error variance; so, as $\sqrt{0.1808}=0.425$, you've got better fit with a log link for this data-set. – Scortchi - Reinstate Monica Jun 10 '19 at 10:09

0 Answers0