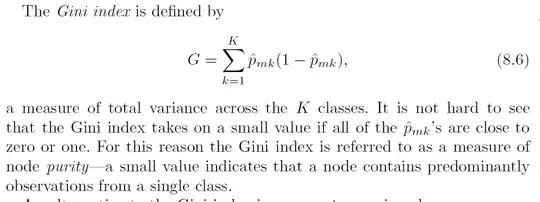I've read many related articles and posts. The more I read, the more I got confused about 'Gini index' and 'Gini Impurity'. I understood the concept but it seems to me that these things are used differently by different people. ISLR book* (page 326) defines Gini Index as $\sum p_i(1– p_i)$ or $1 - \sum p_i^2$.
However, this (and many other articles) [the Same question has been asked in comments too by Shanu_not answered though] compute Gini by $ p^2+q^2$ formula for Binary classifier.
So, their Gini Impurity [ 1 $-$ Gini Index] is exactly the same as the Gini Index computed as per ISLR book.
Please let me know what am I missing. I realize that reading concepts after a long break is painful.
*Gareth James, Daniela Witten, Trevor Hastie, Robert Tibshirani. (2013). An introduction to statistical learning : with applications in R. New York :Springer,