Suppose I am testing whether there is a difference between the mean of two normally distributed variables X and Y, where X ~ N(u_1, 1), Y ~ N(u_2, 1). Is it theoretically correct if I compute the p-value as P(X-Y > delta_xy) if the observed delta_xy is positive, and P(X-Y < delta_xy) if the observed delta_xy is negative? Here delta_xy is the difference between the sample mean of X and Y. In other words, can I do a one-tailed test based on the direction already been observed?
It is of note that if I compute the p-value like this, the "worst" p-value I can get is 0.5, instead of 1. How to explain this?
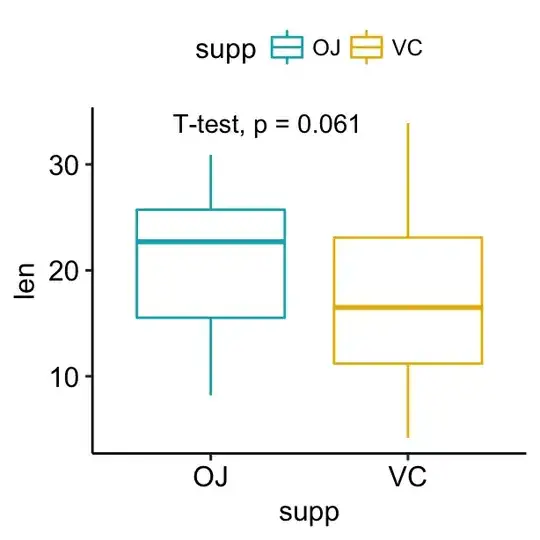
// Following whuber's comment as an "post hoc testing", I give an example as represented in the boxplot, in which we first plot the data and see there is a difference in the mean, most likely we will do a test of mean(OJ) > mean(VC) instead of mean(OJ) != mean(VC), is this an "post hoc testing" abuse?