I have learned that the regression of a random walk process on another leads to seemingly statistically significant relationships, if you just use OLS. However, why do we get such large t-statistics? And why do our usual hypothesis testing mechanisms not work?
In particular, I am looking at regressing one random walk on another. Not just spurious regressions in general.
Consider what random walks are: each new value is just a small perturbation of the old value.
When an explanatory variable $x_t$ and a synchronous response $y_t$ are both random walks, the pair of points $(x_t,y_t)$ is a random walk in the plane with similar properties: each new point is a small random step (in a random direction) from the previous one. This 2D random walk maps the proverbial drunkard staggering in the dark near the lamppost: he will not cover all the ground around the lamppost for quite a while. More often than not, he will lurch off in some random direction and not get around to the other side of the lamppost until first careening off arbitrary distances into the night. As a result, if you plot just a small period of this walk, the points will tend to line up. This creates relations that appear to be "significant."
Ordinary Least Squares (and most other procedures) make the wrong determination of significance because (1) they assume the conditional responses are independent of each other--but obviously they are not--and (2) they do not account for the random (and serially correlated) variation in the explanatory variable. It's the first characteristic that really counts: it will also fool other regression methods designed to account for random variation in the $x_t.$
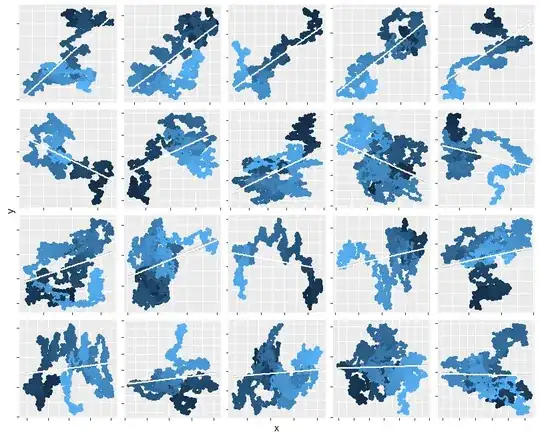
To illustrate this claim, here are maps of 20 separate such walks, each with 30 (Gaussian) steps. To show you the sequence, the starting point is marked with a black dot and subsequent points are drawn in lighter and lighter shades. On each one I have superimposed the OLS fit (a white line segment) and around it is a two-sided 95% confidence interval for that fit. In over half the cases (including all those in the top two rows), that confidence interval does not envelop a horizontal line, indicating the slope is "significantly" non-zero.
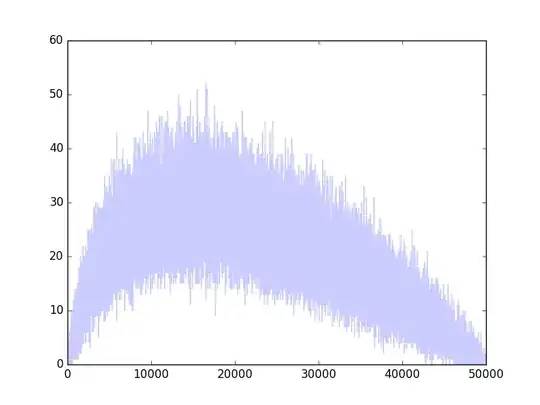
This behavior persists for arbitrarily long times (intuitively, because of the fractal nature of these walks: they are qualitatively similar at all scales). Here's the same kind of simulation run for 3000 steps instead of 30. The R code to generate the figures appears afterwards for your enjoyment. Most of it is dedicated to making the figures: the simulation itself is done in one line.
n.sim <- 20 # Number of iterations
n <- 30 # Length of each iteration
#
# The simulation.
# It produces an n by n.sim by 2 array; the last dimension separates 'x' from 'y'.
#
xy <- apply(array(rnorm(n.sim*2*n), c(n, n.sim, 2)), 2:3, cumsum)
#
# Post-processing to prepare for plotting.
#
library(data.table)
X <- data.table(x=c(xy[,,1]),
y=c(xy[,,2]),
Iteration=factor(rep(1:n.sim, each=n)),
Time=rep(1:n, n.sim))
P <- X[, (p=summary(lm(y ~ x))$coefficients[2,4]), by=Iteration]
setnames(P, "V1", "p-value")
Beta <- X[, (Beta=coef(lm(y ~ x))[2]), by=Iteration]
Beta[, Abs.beta := signif(abs(V1), 1)]
X <- P[Beta[X, on="Iteration"], on="Iteration"]
setorder(X, `p-value`, -Abs.beta, Iteration)
#
# Plotting.
#
library(ggplot2)
ggplot(X, aes(x, y, color=Time)) +
geom_point(show.legend=FALSE) +
geom_path(show.legend=FALSE, size=1.1) +
geom_smooth(method=lm, color="White") +
facet_wrap(~ `p-value` + Iteration, scales="free") +
theme(
strip.background = element_blank(), strip.text.x = element_blank(), axis.text=element_blank()
)
It's not always a problem when both dependent and independent variables are random walk. If two variables are cointegrated then you still can run OLS. It won't be the best choice, but it will retain its good properties.
So why is it a problem sometimes? In a random walk you get the variance increasing with time proportionally. Moreover, you can set any arbitrarily large value and there's non zero probability that random walk process will cross it at some point. So, if you get two sufficiently long samples of independent random walk processes, it is very high probability that there will be a "fake" trends detected in both of them even if their drifts are zero. Simply because it is very high probability that at the end of the series they will be quite far from where they started - this will look like a trend (drift). Once you have two trends, there will be correlation, a spurious (fake) one.
