Given that I just have a correlation matrix ($X$ Variables vs. $Y$ Principal Components), and that I am trying to find 2 missing eigenvalues (e.g., missing $\lambda_1$ and $\lambda_5$) from the total $X$ eigenvalues. How should I proceed?
Asked
Active
Viewed 23 times
2
-
Not sure I understand the set up. Do you have an n by n correlation matrix and know some of the eigenvalues of the covariance matrix? Take for instance the correlation matrix being the 2 by 2 identity matrix with one of the eigenvalues being known, if the smaller eigenvalue is known, the larger eigenvalue could be any number $\ge $ that. If the larger eigenvalue is known, the other can be any number $\le $ that and $\ge 0$. – Mark L. Stone Jun 15 '19 at 23:36
1 Answers
1
If you have the remaining eigenvales, then you can try to interpolate. This will not work for missing $\lambda_1$, of course, but may work well for other eigenvalues.
You can try using Marchenko-Pastur distribution like in this answer.
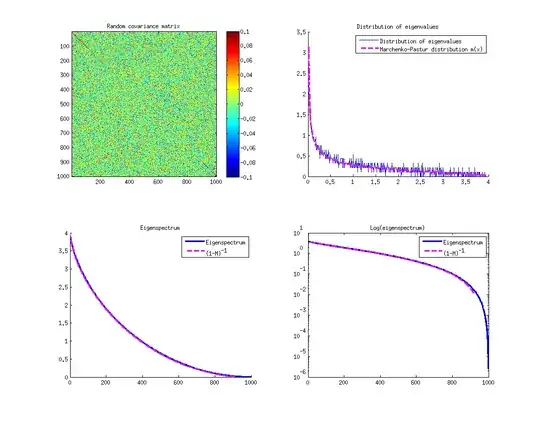This distribution concerns eigenvalues of random matrices, particularly, large ones. I would think it can help filling the blanks by providing you with a shape of eignevalues spectrum.
Aksakal
- 55,939
- 5
- 90
- 176