2

I'm seeking a little clarification on the specific application of transfer functions for time series.

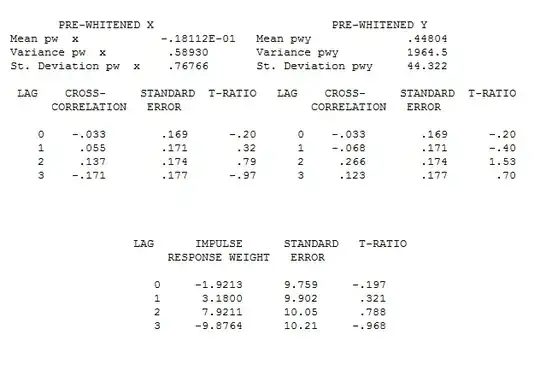
I've followed the Box-Jenkins approach for selecting potential exogenous predictors... using R's prewhiten function to "identify" the independent time series and then filter the Y and check for significant lags in the CCF plot. Let's assume that in doing so, a statistically significant lag was found for all predictors. yay!

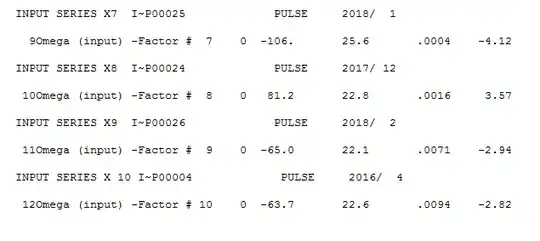
However, when I plug all variables into the full transfer function model, I find that I have to make adjustments to the individual Transfer Function parameters of each IV in order to 1) lower the BIC and 2) obtain statistically significant p-values. I'm mostly adjusting the delay parameter of the transfer functions - the Numerator and Denominator terms are mostly the same based on their ARIMA identity.

Am I doing something wrong? Is this the "subjectivity" Pankratz mentioned...

as an example, let's say one IV has the form: (1,0,1), and significant CCF with y at lag 6 - found using the prewhitening operation. However, once in the model with other variables, I may have to change that delay from 6 to 4 or to 0 in order for the variable to be statistically significant or see a drop in the BIC.

maybe this is not really allowed? I'm not sure.

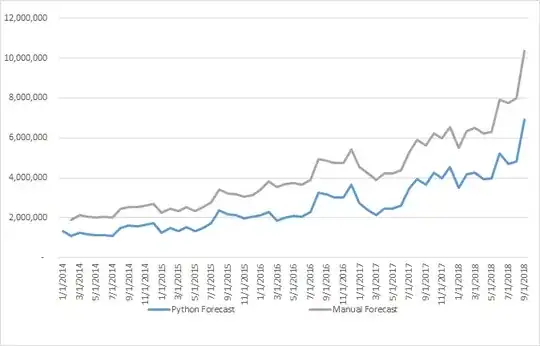
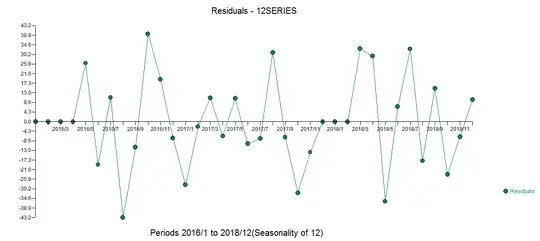
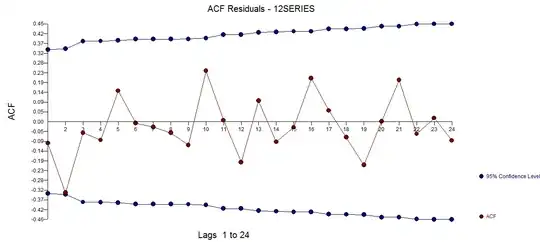
However... using this "subjective" approach, I was able to fit a nearly perfect model with a MAPE (yes I know about the problems) of less than 1% and all predictors being statistically significant and an 3-point reduction in BIC. believe me, I'm not that good at this.

Thank you, as always.

EDIT 1:

data can be found here: Data

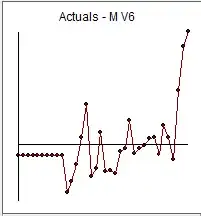
image of the final multivariate transfer function enter image description here

image of the model summary statistics enter image description here

model residuals enter image description here

logisticregress
  • 127
  • 9
  • Why don't you post tour data so we can feel your pain and try to offer a little relief. – IrishStat May 25 '19 at 23:10
  • the data cannot be posted in public forums per the NDA that was signed. Since, this is more of a process question, and I provided some of the technical statistics from the model, I was more inviting a conversation around the process and assumptions, rather than inviting re-analysis of the data. – logisticregress May 26 '19 at 16:49
  • if you want to have a dialogue ..be glad to ... you an contact me at 215-394-8897 as It is impossible for me to have one-way discussions as there is a lot here to learn. – IrishStat May 26 '19 at 18:04
  • if you can't post your data then doubly scale it to hide the original. – IrishStat May 26 '19 at 19:10
  • I've posted the scaled data and a screenshot of the model. The transfer functions were built after identifying significant cross correlationsn between each IV and the DV. – logisticregress May 30 '19 at 02:01
  • Can you please post a screen shot of your model residuals versus time and also post these residuals in a csv file as that is often of interest in reviewing models. – IrishStat May 30 '19 at 07:17
  • residual ACF/PACF plot added – logisticregress May 30 '19 at 14:51
  • perhaps lag 6 is being induced .....just a surmise as I have seen where over-modeliing leads to spurious counter arguments.;;;think SLUTSKY – IrishStat May 30 '19 at 15:00

1 Answers1

1

Following the broad guidelines laid out in The theory behind fitting an ARIMAX model I introduced your 36 monthly values and 12 time series into AUTOBOX. After the AUTOBOX modelling process http://www.autobox.com/pdfs/A.pdf is followed I will briefly critique the differences between your over-parameterized SAS model and the AUTOBOX result.

To begin with I scaled the output series (your DV) by 1000 to make the data more commensurate, probably unnecessary but as a safety measure. Following is the graph of the DV enter image description here and a curious V6 showing that early values were assumed to be constant rather than reverse forecasted enter image description here.

Transfer Function Model Identification is not done by "identifying significant cross correlations between each IV and the DV" but rather by employing pre-whitening filters to compute pre-whitened cross-correlations for identification purposes. I believe that this important/critical feature was not available to you in the software you used BUT I am not a SAS expert.

For completeness purposes I present the pre-whitened results here for V6 . Here are the two filters )one for V6 the other for Y enter image description here and the pre-whiteningenter image description here results . Notice that the differecing opertaor for V6 is a 1 reflecting the systematic effect of a set of constants in the history of v6.

AUTOBOX developed the following model enter image description here and here enter image description here and enter image description here . It used 6 predictors and 4 identified pulse anomalies (curious that the three periods 25,24 and 26 were on the list !) along with a constant (11 parameters in total based upon 33 estimable equations) to obtain enter image description here

The base 36 values (Y) were filtered to obtain the following residual plot enter image description here with an acf here enter image description here .

The Actual/Fit and Forecast is here enter image description here with Actual/Cleansed here enter image description here

CRITIQUE (GENTLE !) OF YOUR MODEL AND MODELLING APPROACH:

1) The data should be scaled to make it more commensurate to avoid possible numerical estimation issues.

2) Missing early value should be reverse forecasted rather than using a constant

3) Identification is done with pre-whitened data

4) You had 36 observations . You used a model for V6 (delay 9 + first differences) which effectively dropped the number of estimable equations to 26 (36-9-1) which you then used to estimate 17 parameters yielding 9 degrees of freedom. This in my opinion is wildly over-fitting and is responsible for the r-sq of .994 ( as compared to AUTOBOX's .769 ) that you reported .... which you were questioning anyway.

I believe your r sq of .994 (26 estimable equations ...17 parameters) lead you to say "I was able to fit a nearly perfect model with a MAPE (yes I know about the problems) of less than 1% " . This is an unfortunate result of excessive parameterization using a targeted approach as you sought out cross-correlations to be fit.

5)The p values of 0.0000 for your 17 estimated parameters should have been a red flag for you ( and probably were !)

6) Modelling lags of 7,8,9,10 etc periods with 36 observations for monthly data is a bit much and probably spurious unless supported by prior domain knowledge.

All of my comments here are made in good faith to help you and others better understand the transfer function modelling approach and the impact of available software on that.

IrishStat
  • 27,906
  • 5
  • 29
  • 55
  • thanks for the comprehensive review. I should re-iterate that I in fact used R's pre-whiten function to identify significant cross-correlations. 1. I used scaled data when constructing the transfer functions 2. I used reverse forecasting, and a constant value was the best "forecast" found 3. see 1 above. 4. yes, I was afraid of that 5. it was. 6. agreed, although the domain is a slow moving industry... it could make sense. – logisticregress May 30 '19 at 14:16
  • for pre-whitening, I followed the method outlined here: https://newonlinecourses.science.psu.edu/stat510/lesson/9/9.1 I first used auto.arima to identify each x: x_a – logisticregress May 30 '19 at 14:46
  • My main question was in regard to adjusting the delay parameters in the transfer function to coerce statistical significance. If I change a delay parameter from 1 to 2, for example when the pre-whiten CCF clearly said the significant cross correlation is at 1. – logisticregress May 30 '19 at 14:55
  • i would not be changing the delay ..... this is perhaps an over-read ....easy to do !. – IrishStat May 30 '19 at 14:58
  • it might be helpful if you could elaborate on the reason why... – logisticregress May 30 '19 at 15:04
  • I would have to see specifics before I could fully answer. You can contact me offline and we can set up a SKYPE so that I can be less ambiguous and hand-waving and vaguely broad. – IrishStat May 30 '19 at 15:12
  • just a fine point ....AUTOBOX automaticall builds and uses the pre-whitening features ( valuable front end) and automatically adds intervention variables (pulses,seasonal pulses ,level shifts and local time trends) to the model as needed ( valuable back end ) prior to validating the homogeneity of the error variance over time . – IrishStat May 30 '19 at 18:34
  • Is it not time to upvote my answer and to accept it and to close the question in order to bring awareness from the list ?. AND I repeat if I can be helpful in discussing strategy .. glad to be of help in freely passing on some of my hard-earned wisdom. – IrishStat May 30 '19 at 21:36
  • two comments: the Autobox output is virtually unreadable. secondly, it found all the variables to be statistically significant and I don't see how Autobox is using transfer functions for the IVs. – logisticregress May 30 '19 at 21:54
  • Let's do a skype .or simply call me on my land line 215-394-8897 . AUTOBOX only retained 6 of the IV;S and added 4 pulse inputs .. it discarded 4 of your IV'S – IrishStat May 30 '19 at 22:23
  • The 6 IV'S found to be significant were purely numerator in form . one had differencing , two had delays . . – IrishStat May 30 '19 at 22:27
  • have I cleared things up with these one-directonal reflections ? perhaps a chat room would help ? – IrishStat May 31 '19 at 16:03