We can extend the reasoning presented in Can a random forest be used for feature selection in multiple linear regression? to this context.
The data in this figure are obviously separated by the circle $1=x_1^2 + x_2^2$, which is a nonlinear boundary in $x_1, x_2$. 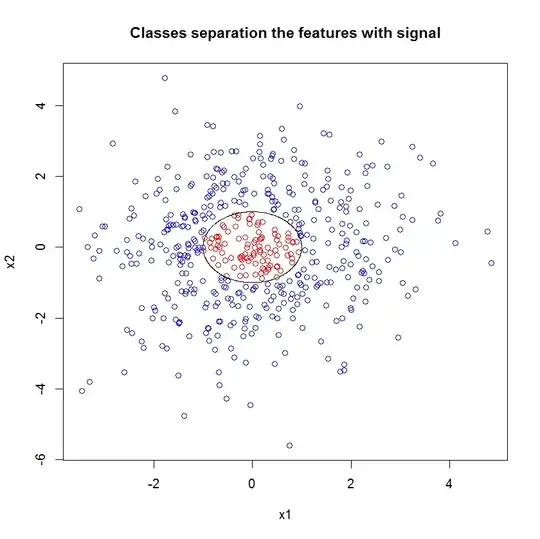
Because the relationship is pretty obvious, it shouldn't be surprising that random forest can do a good job of picking out some approximation to this boundary.
On the other hand, a linear model, such as a logistic regression, has the form $$\mathbb{P}(y=\text{red}|x)=f(\beta_0 + \beta_1 x_1 + \beta_2 x_2).$$ Even though $x_1, x_2$ have a nonlinear relationship to the outcome, this linear model can't recognize the relationship between $x_1, x_2$ because the relationship is nonlinear. In order for the linear model to find this relationship, you would have to specify the model such that the features are related to the outcome using a linear form, perhaps an indicator variable that takes the value 1 whenever $x_1^2 + x_2^2 < 1$. It's easy enough to do this here, when we can visualize the data readily. But with noisy data and many features, it's much harder to carry out this transformation. This is the appeal of random forest and similar methods: they can find relationships between features and outcomes with little human intervention.
In fact, because the boundary has the form $1 = x_1^2 + x_2^2$, it is nonlinear and it depends on two features acting together; if $x_1^2$ is small, that is not sufficient for a point to be Red because $x_2^2$ may be large, and all Red points must be small enough in both $x_1^2$ and $x_2^2$.
All of this is a very detailed way to say that what a model considers important is specific to the model itself, and not "universal." Differences in how models go about estimation strongly bear on how the model assigns importance.
There are a number of other caveats around random forest feature importance, beyond the fact that it is not comparable to importance as measured by a linear model. For more information, https://explained.ai/rf-importance/index.html
Additionally, some criticism of interpreting larger coefficients as more important can be found in Gary King, "How Not to Lie with Statistics: Avoiding Common Mistakes in Quantitative Political Science"
