Are there advanced "cos similarity" that influence of dim size is less?

Question

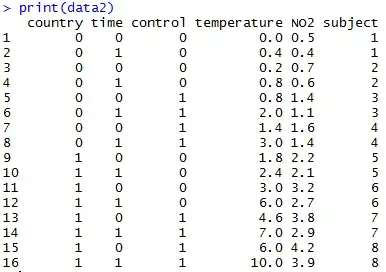
I found that the cosine similarity is affected to the effect of "Curse of dimension" by trying the following simulation.

1. create(select) two vectors form uniform random numbers U[-1, 1], each dim = 2, 3, 4, 5, 6, 7, 8, 9, 10, 100.

2. calculate cosine similarity form the two vectors.

3. repeat step1 and 2, N = 100,000 times, then create histograms.

Thinking by naive sense, "cosine similarity" should also be uniformly.

But actually result in the following figure. This shows that the "value of similarity" is clearly different by changes of dim size.

for example,

• In dim=2, similarity of pairs of about 10%(10,000/100,000) vectors is [0.95-1] even if randomly select two vectors; while dim=10, it's 0% (because cross axis is too many)

(I do not know the reason well that there are many parallels such as -1 or 1 when dim=2)

Are there other alternatives similarities such as being less this effect of "Curse of dimension" ?

Reproduction code:

import scipy as sp
import scipy.stats as stats
import scipy.spatial as spatial
import matplotlib.pyplot as plt

dims = sp.array([2, 3, 4, 5, 6, 7, 8, 9, 10, 100])
uniform = stats.uniform(loc=-1, scale=2)
def cos_sim(vec1, vec2):
    return 1 - spatial.distance.cosine(vec1, vec2)

def get_cos_sim_array(count, dim):
    cos = sp.zeros(count)
    for i in sp.arange(count):
        vec_1 = uniform.rvs(dim)
        vec_2 = uniform.rvs(dim)
        cos[i] = cos_sim(vec_1, vec_2)
    return cos

n = 100000
bins = sp.linspace(-1, 1, 40+1)
fig = plt.figure(figsize=(16, 12))
for i, d in enumerate(dims):
    cos = get_cos_sim_array(n, d)
    ax = fig.add_subplot(round(len(dims)/2), 2, i+1)
    ax.hist(cos, bins)
    ax.set_title(f"dim = ${d}$", fontsize=20)
    ax.grid()

plt.tight_layout()
plt.savefig("cos_sim.png")
plt.show()