2

I am trying to transform my GARCH standardized residuals to PITs in order to use them in a copula. The following code has been so far applied:

gjr_garch = arch_model(log_r['DAX'].dropna(), mean='AR', lags=8, vol='garch', p=1, o=1, q=1, dist='t')
dax_test = gjr_garch.fit()
dax_test.summary()
dax_dof = dax_test.tvalues['nu']
dax_sigma = dax_test.conditional_volatility
dax_innovations = dax_test.resid / dax_test.conditional_volatility
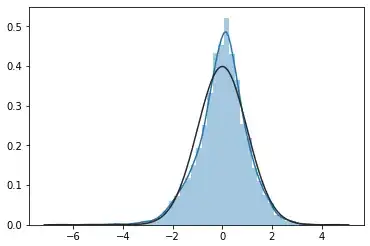
dax_innovations_std = (dax_innovations - np.mean(dax_innovations)) / np.std(dax_innovations)

enter image description here

sns.distplot(dax_innovations_std.dropna(), hist=True,fit=stats.norm)

enter image description here

Next, I just take the CDF of the standardized innovations with their respective d.o.f. estimated by the GARCH model. 

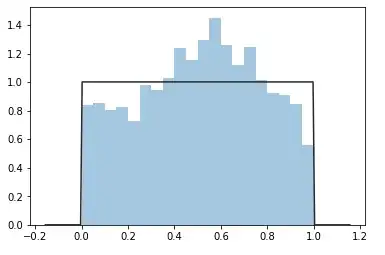
dax_uni = t.cdf(dax_innovations_std, dax_dof)

I convert them to pd.Series just so I can dropna()

dax_uni = pd.Series(data=dax_uni)
sns.distplot(dax_uni.dropna(), bins=20, fit=stats.uniform, kde=False)

enter image description here

In fact, I've done this for not only GJR-GARCH but also for AR-TARCH AR-EGARCH models with AR means ranging from 0 to 10. None of the Probability Integral Transforms pass the Kolmogorov-Smirnov test for Unif(0,1).

Any ideas why can't I get uniformly distributed probability transforms?

deblue
  • 53
  • 5

1 Answers1

3

This is because your model is not perfect. Models are always mispecified and, consequently, the (estimated) residuals do not perfectly resemble a normal or t distribution. Thus, transforming the residuals using a t or normal distribution would not lead to a uniform sample, as it happens when you transform $F^{-1}\circ G$ (not the identity function) instead of $F^{-1}\circ F$ (the identity function).

Clegane
  • 31
  • 1
  • I was thinking the same however, even thought the model is not perfect, it still estimates the degrees of freedom pretty accurately doesn't it? Doesn't this mean that even though the model is imperfect, the empirical distribution is pretty much fit by the t-distribution with the estimated d.o.f. and, as such, should result in Unif(0,1) PITs? – deblue May 14 '19 at 14:37
  • @SergejShteriev The fact that you can estimate the parameters accurately does not mean that the model is good. This happens because the estimator is consistent, but it only converges to the model that better resembles the true distribution of the data. If you simulate from an asymmetric model but you fit an symmetric model, you will get accurate estimates with large samples, but you will never be able to resemble the asymmetry of the data as your model is symmetric. The same happens with other characteristics such as multimodality, heavy tails, or more complex ones such as heteroscedasticity. – Clegane May 14 '19 at 14:40
  • What would you recommend for me to do to get more accurate PITs? I am guessing I'd have to model the heavy tails somehow? – deblue May 14 '19 at 14:50
  • @SergejShteriev The problem seem to be a bit in the mid range of the sample, probably some repeated observations. Thus, using an exponential power distribution instead of $t$ may help. However, this model may not be implemented in your software. However, the problem might go beyond the choice of the distribution of the residual errors as it may be the presence of heteroscedasticity or mispecification of the autoregressive part, or the linearity, and etcetera. Parametric model selection is an art. I wish you luck and have fun trying to find a good model for your data! – Clegane May 14 '19 at 14:56
  • Thank you very much for the useful comments! I'll give a shot with a GDE (it is actually available in arch_models()) and see if I get somewhat more precise results. In regards to the heteroscedasticity however, isn't the covariance HAC in the arch_models as stated on the bottom of the summary table? – deblue May 14 '19 at 15:29