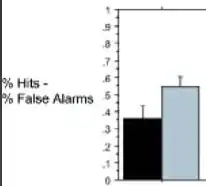
What is lost/missed out on if defining d', the sensitivity index from Signal Detection Theory, based on non-standardised rates?
For example, Patel et al. 2008, for a task where normal and anomalous chords have to be discriminated, define performance as simply the HR-FAR difference, instead of z(HR)-z(FAR), although granted they don't claim that this difference represents d'.
It seems that if using non-standardised (hit and false-alarm) rates as in this paper, nothing changes with regards to chance level responding, which is still 0, just as in the case of standardised rates (d'). However, ceiling-level responding, i.e. maximal performance (hits 100%, false alarms 0%), now neatly corresponds to 1, whereas with standardised rates, the ceiling d' depends on which approximation one chooses to avoid the division by zero problem (details here), but is in either case a non-round (and 'arbitrary-looking') number.
Assuming the advantage of using non-standardised rates is in fact this - namely having a convenient range of performance values (0 and 1) for chance and ceiling respectively - then the question is: is there also a disadvantage or cost to non-standardised rates?
Reference:
Patel, A. D., Iversen, J. R., Wassenaar, M., & Hagoort, P. (2008). Musical syntactic processing in agrammatic Broca’s aphasia. Aphasiology, 22(7–8), 776–789. https://doi.org/10.1080/02687030701803804