2

Suppose you observe a random $p$-vector $X$ which follows an elliptical distribution with mean zero, covariance $\sigma^2 I$ and (unknown) distribution function $g$. Given a single observation of $X$, how would you estimate $\sigma$?

Note that when $X$ is Gaussian, the marginals of $X$ are independent, and the usual sample estimate of variance, namely ${X^{\top}X / p}$, is unbiased and efficient (in $p$) with a standard error that is $\mathcal{O}\left(p^{-1/2}\right)$. However, for other elliptical distributions, the standard error of this estimator does not decrease to zero in $p$, but rather has an irreducible contribution from the kurtosis of the distribution. Using Isserlis' Theorem for Elliptical Distributions, you can show that the standard error of $s^2 = X^{\top}X/p$ is equal to $$ \sigma^2\sqrt{(\kappa - 1) + \frac{2\kappa}{p}}, $$ where $\kappa$ is the 'kurtosis factor', equal to one-third the kurtosis of the marginals. For the Gaussian case, $\kappa=1$, but $\kappa>1$ for fatter tailed elliptical distributions.

A demonstration:

library(mvtnorm)
library(dplyr)
library(tidyr)
library(ggplot2)

sigsq <- 0.5

nsim <- 5000
psize <- unique(ceiling(exp(seq(log(4),log(512),length.out=17))))
set.seed(12532)
empvars_gauss <- sapply(psize,function(p) {
  rsamp <- rmvnorm(n=nsim,sigma=sigsq*diag(p))
  var(rowMeans(rsamp^2))
})
nu <- 6
set.seed(23521)
empvars_td <- sapply(psize,function(p) {
  rsamp <- rmvt(n=nsim,sigma=sigsq*((nu-2)/nu) * diag(p),df=nu)
  var(rowMeans(rsamp^2))
})
data_frame(p=psize,gauss=empvars_gauss,td=empvars_td) %>%
  tidyr::gather(key=distribution,val=empvar,gauss,td) %>%
  mutate(exkurt=ifelse(distribution=='gauss',0,6/(nu-4))) %>%
  mutate(kappa=(exkurt + 3)/3) %>%
  mutate(se=sigsq*sqrt((kappa - 1) + (2/p)*kappa)) %>%
  ggplot(aes(p,sqrt(empvar),color=distribution)) + 
  geom_point() + 
  geom_line(aes(y=se)) + 
  scale_y_log10() + scale_x_log10() +
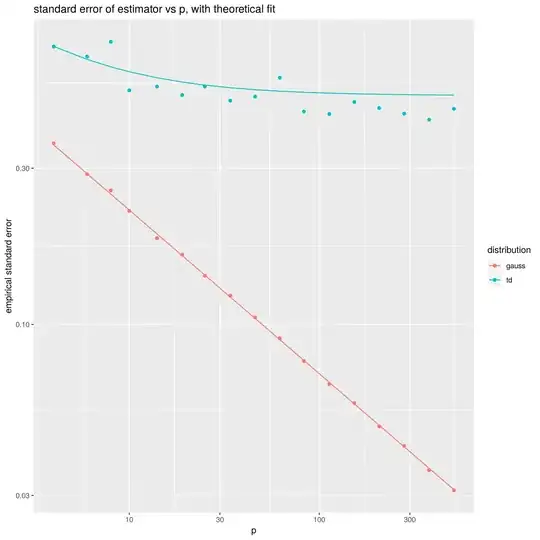
  labs(title='standard error of estimator vs p, with theoretical fit',
       x='p',y='empirical standard error')

enter image description here

shabbychef
  • 10,388
  • 7
  • 50
  • 93
  • Because your plot clearly does show a decrease in standard error as $p$ increases, could you elaborate on your observation that "the standard error of this estimator does not decrease in $p$"? – whuber May 06 '19 at 14:26
  • @whuber you are right that the demonstration was ambiguous as I had previously noted. I have edited to include the theoretical standard error of $s^2$ which matches the empirical standard error fairly well. (well, it matches better for larger $\nu$, which I suspect is a limitation of `rmvt`.) – shabbychef May 07 '19 at 04:56
  • 1
    I should note that taking the median of the $p$ squared marginals seems to have lower standard errors, but I believe is biased. Moreover, this median estimator does not seem to have standard error which is $\mathcal{O}\left(p^{-1/2}\right).$ – shabbychef May 07 '19 at 05:09

0 Answers0