-14

It seems these terms are confusing. Some experts think that these terms have a contrasting meaning which is incorrect. Is there someone who can justify the interpretation.

  • 12
    They are opposites. – Michael R. Chernick May 04 '19 at 18:24
  • Homoscedasticity term is used to represent dispersion in continuous data. The term heteroscedasticity measures dispersion of binomial-effects (here in terms of extent of skewness) e.g. treatment of patient results in success i.e. 1 or failure I.e. 0. I have stated in my answer 0, 1 type of data. In case of meta-analysis, we have data of this type and proceed with moderated regression using one or more possible moderator variables as independent variables. thanks for comment. –  May 05 '19 at 02:41
  • 5
    I don't buy your explanation. "Homo" means the same or similar . "hetero" means diverse.. – Michael R. Chernick May 05 '19 at 14:43
  • thanks a lot for your comment. I agree with you (upvote). Howevever, I disagree with the classfication - opposites. –  May 05 '19 at 15:52
  • My rework tells me that we can not or should not use linear regression. We can simply invoke GLM in case of homoscedastic data with a minor change in GlM model i.e. mulltiply the term reflecting beta(X) by p-correlation. I shall change the answer. –  May 05 '19 at 16:06
  • 5
    The experts are correct and there is no confusion at all. – Peter Flom May 06 '19 at 10:57
  • These terms are not contrasts in meaning. The homoscedasticity measures dispersion first and then checks for equality or inequality of dispersion among several groups. Heterocedasticity measure computes dispersion/skewness for groups. Each measure finally tells how many groups are similar (and how many are dissimilar). Thus, Heterogeity shows no. of groups that hetero - disimilar and remaining are similar). The intensity of heterogeneous reflects heterogeneity. –  May 06 '19 at 11:09

2 Answers2

12

They are opposites. skedasis means “dispersion”, so hetero mean different variances and homo indicates same/constant variances of the distribution where the shocks/errors/disturbances come from.

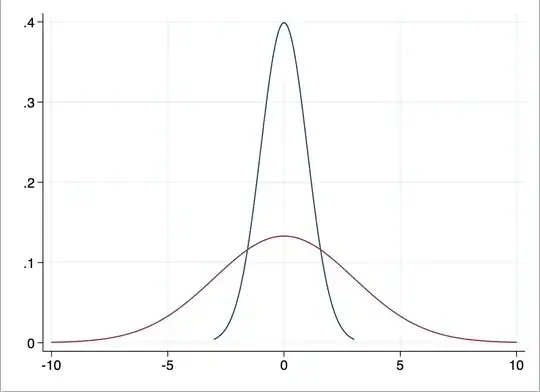
For example, if some observations get their errors from the blue distribution (lower variance), while others are drawn from the red (higher variance), you have heteroskedasticity.

enter image description here

dimitriy
  • 31,081
  • 5
  • 63
  • 138
  • Is there any distinction between dispersion and skewness ? –  May 04 '19 at 00:58
  • 2
    @SubhashC.Davar Skew is about the asymmetry of the distribution about the mean, variance is about dispersion around the mean. For a unimodal distribution, negative skew means there is a long tail is on the left side of the distribution, and positive skew indicates that the long tail is on the right. – dimitriy May 04 '19 at 01:52
  • @dimitriy-v-masterov Sir, your interpretation of skedasis is incorrect. Please recheck it. –  May 06 '19 at 11:33
  • @SubhashC.Davar See [here](http://www.perseus.tufts.edu/hopper/morph?l=ske%2Fdasis&la=greek&can=ske%2Fdasis0). As any thesaurus will tell you, scattering and dispersion are synonyms. If you continue to maintain that your interpretation is correct, please link or cite some authority on the matter that supports your view. Acting like Humpty Dumpty will not help in this instance. – dimitriy May 06 '19 at 15:10
  • Define scedastic 2. (Statistics) (of a bivariate or multivariate distribution) having one variable whose variance is the same for all values of the other or others. 3. (Statistics) (of a random variable) having this property. Homoscedastic - definition of hom… www.thefreedictionary.com/homoscedastic –  May 06 '19 at 15:42
  • "whose variance is the same for all values of the other or others." Is it sufficient to support my viewpoint ? –  May 06 '19 at 15:52
  • 4
    @SubhashC.Davar I don't see anything at that link that contradicts what I wrote, and I have nothing more to add to the discussion here. Best of luck! – dimitriy May 06 '19 at 16:00
  • The link above clearly points out the property - Homoscedastic if you have two or more explainatory variables and one of the two is scedastic. –  May 06 '19 at 16:12
  • 1
    I would add that there is no need to specify errors, shocks or disturbances. Two or more distributions are homoscedastic if they have the same variance and heteroscedastic otherwise. It's likely true that errors in regresssion-type models provide the most common context for using these terms, but in principle they apply generally. – Nick Cox May 07 '19 at 10:08
  • 3
    @SubhashC.Davar To what has been said to you many times, I add just two further points. I can't see any _useful_ meaning at all to the word "scedastic" without prefix. If it means anything it just means variable, which is useless, because the word variable is already in use and simpler for most people not Greek. Also homo- or heteroscedasticity has nothing whatsoever to do with skewness. If you can cite literature that says so, that would be a public service, as you would be flagging a paper or textbook to avoid. – Nick Cox May 07 '19 at 10:13
  • esteemed , Mr. Nick please go through comments carefully and you will be able to trace the source that tellls meaning of scedastic. For the meaning, you may read two comments under Dimitriy V. Masterov.. I shall explain homo and hetero in a specific context. I can not disclose everrthing. –  May 07 '19 at 11:07
  • 6
    Subhash, you had to look hard for an inferior definition of "homoscedastic" and even then you chose to cite the least relevant of the definitions offered. Using selective quotations from unauthoritative sources to confront people (who are trying to help you out of your confusion) and to call them wrong is likely to offend anybody. Even when people are not affronted by your attitude, I'm sure they will learn not to answer any more questions you might post. – whuber May 08 '19 at 03:35
  • 2
    Any good English dictionary explains that _homo_ and _hetero_ are standard Greek roots, from words meaning the same or different respectively. They are in use for many words more common than homoscedastic or heteroscedastic. The thread https://stats.stackexchange.com/questions/153526/why-are-there-two-spellings-of-heteroskedastic-or-heteroscedastic comments on their origin and use in statistics. I doubt that I can add anything else that will be helpful. There are many problematic terms in statistics, but these aren't among them: the definitions are agreed and simple. – Nick Cox May 08 '19 at 07:52
-2

They are actually opposite!

Think, for instance, of a linear model where $Y=\beta_0 + \beta_1 x + \epsilon$ where $\epsilon$ is constant. Here you have homoskedasticity, since variance will always be the same, regardless of $x$

If $\epsilon$ depended on the values of $x$, you would have heteroskedasticity, with the variance being different depending on the value of the regressor

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
David
  • 2,422
  • 1
  • 4
  • 15
  • 6
    I don't think this is quite right. If the epsilons come from distributions with different *variances*, you have heteroskedasticity. This does not require dependence on $x$ (though that is common) and epsilon is definitely not constant. It is a random variable, with varying or constant variance. – dimitriy May 03 '19 at 23:53
  • 2
    @DimitriyV.Masterov Right. Your point about the variance of $\epsilon$ is especially apt. David I think means that the variance of the distribution of $\epsilon$ is constant *a la* $\epsilon \sim \mathcal{N}(0,\sigma_{\epsilon})$, where $\sigma_{\epsilon}$ is some constant value. – Alexis May 04 '19 at 04:09
  • I was just giving an example. You can have heteroskedascity in many different situations, not even necessarely in linear regression – David May 04 '19 at 08:25
  • 5
    You probably mean that the variance of e is constant, not e itself. – Michael M May 06 '19 at 08:37