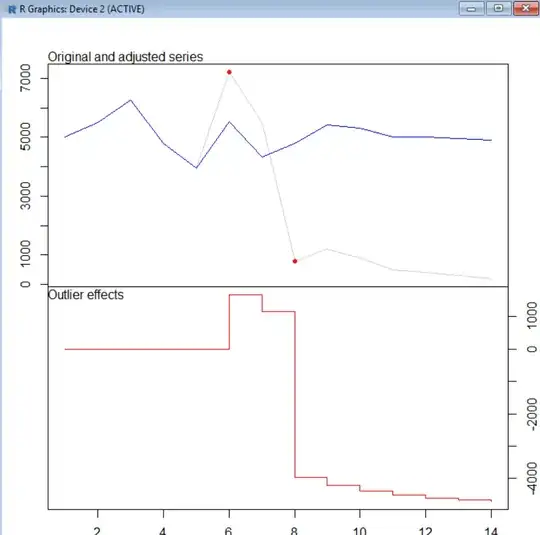
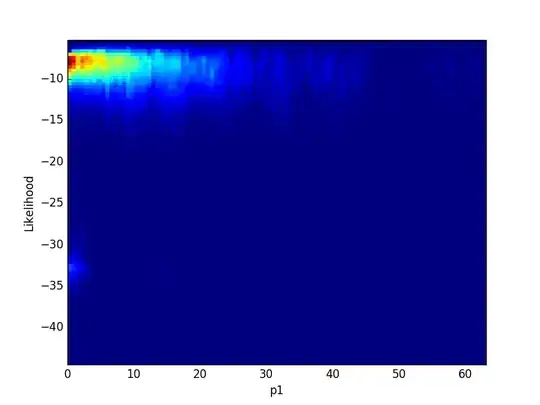
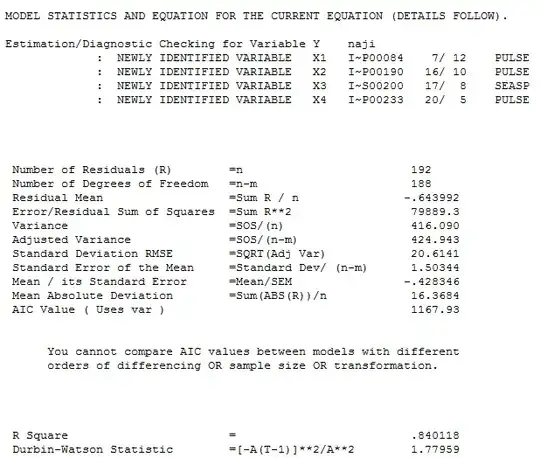
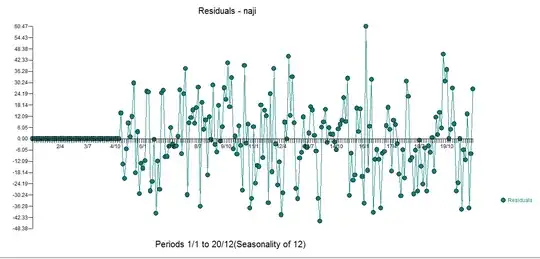
I am trying to attain an ARIMA model for the following Time Series Data:
There is quite obviously a seasonal component - as the plot seems to oscillate between smaller and larger peaks, its seems to suggest that the pattern repeats every 48 timesteps.
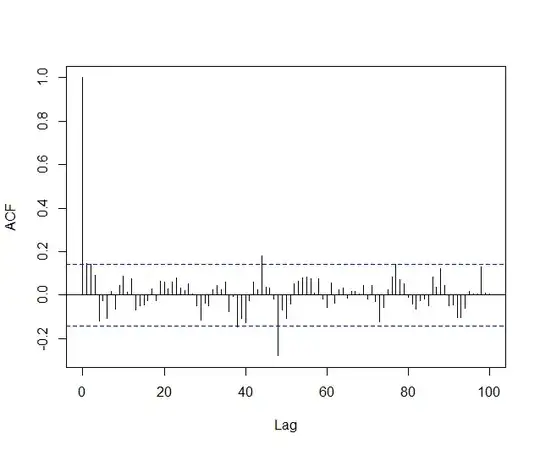
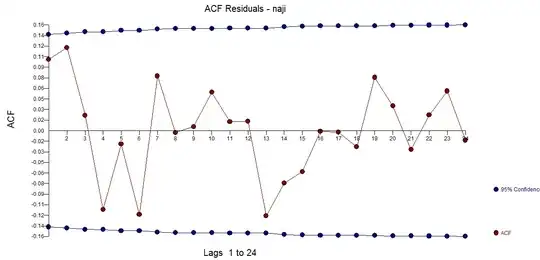
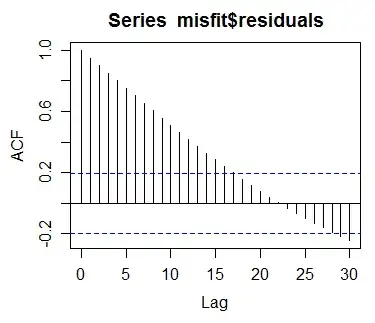
I then took the seasonal difference and plotted the ACF & PACF:
From the ACF & PACF plots, I concluded that the model will most likely fit a $\text{ARIMA}(0,0,1)(0,1,1)_{48}$ model due the the shape of the PACF and the peaks at the ACF plots.
However, when trying to fit the data onto such model, the estimated coefficient for the regular fails the hypothesis test (roughly if $\mid\frac{\hat{\theta}}{\hat{\sigma}_\theta}\mid > 1.96$, then accept for some coefficient $\theta$).
I have tried other variations, but they consistently fail. I have come to the conclusion that I've made a grave error or I am missing a step. Note that when using Regular Differencing, the model does seem to fit better - but I don't know how to justify using Regular Differencing.
I have come to one of two conclusions: Either taking the seasonal difference of 48 is too high, or, the plot for PACF shows that the data may be non-stationary - therefore needing some Regular differencing.
Thank you