Power calculations

Question

I am using a toy example to explain power calculations for a t-test

Let's say we have two populations where we measure a certain parameter. Population A has a mean of 0 and population B has a mean of 3, both with a sd of 2. The effect size is 1.5

I use the pwr package in R to do the power calculation as such

library(pwr)

pwr.t.test(n = NULL, d = 2/3, sig.level = 0.05,
           power = 0.9, type = "two.sample",
           alternative = "two.sided")

Two-sample t test power calculation 

          n = 48.26427
          d = 0.6666667
  sig.level = 0.05
      power = 0.9
alternative = two.sided

NOTE: n is number in *each* group

So, R is suggesting 48 observations per group, to get a power of 0.9

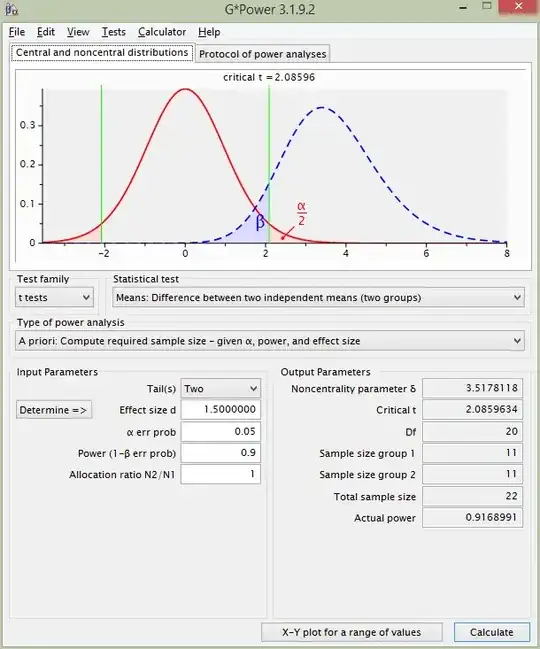
If I repeat the calculation using G*Power, however, I get this, which suggests 11 observations per group!

Finally, if I use this online tool from the University of British Columbia I get 10.

I can understand that rounding errors may bring you from 10 to 11... but why is R giving me such a high value?

Indeed, if I do a little simulation, it looks like 10 or 11 observation give you a power of ~90%

n <- 10

res <- sapply(1:1000, function(x)
  {
  a <- rnorm(n, 0, 2)
  b <- rnorm(n, 3, 2)
  res <- t.test(a, b, alternative = "two.sided")
  res$p.value
  })

table(res<=0.05)

FALSE  TRUE 
  115   885    <-- 88.5% power

n = 48 always gives me a power of 100%... am I missing something?

In R, you use an effect size of 2/3 = 0.66 whereas in G\*Power you use 1.5. If you use $d=1.5$ in `pwr.t.test`, I get an *n* of $10.4$ which, rounded up is $11$ and coincides with G\*Power. — COOLSerdash, Apr 25 '19 at 11:30

COOLSerdash · Accepted Answer · 2019-04-25T11:42:03.710

In your example using R, you're using an effect size of $d=2/3\approx0.6667$ whereas in G*Power, you're using an effect size of $d=1.5$. Repeating the calculations in R using an effect size of $1.5$ results in comparable results:

library(pwr)

pwr.t.test(n = NULL, d = 3/2, sig.level = 0.05,
           power = 0.9, type = "two.sample",
           alternative = "two.sided")

     Two-sample t test power calculation 

              n = 10.40147
              d = 1.5
      sig.level = 0.05
          power = 0.9
    alternative = two.sided

NOTE: n is number in *each* group

As you would round the sample size up, both R and G*Power suggest using a sample size of $11$ per group.

I knew it was a silly mistake! I wrote 2/3 instead of 3/2... thank you for spotting that! — nico, Apr 25 '19 at 11:46

Power calculations

1 Answers1