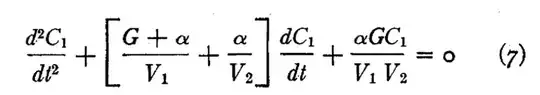BTW the link is broken. If one takes $y_0=0$, and $x$ to be time, $t$, the equation refers to a particular solution to the second order linear differential equation with constant coefficients using maximum initial functional value (at $t=0$). The reason for the simplifying assumption of $y_0=0$ is to formulate the answer as a density function, as a density function requires a finite area under its support. It is possible in some circumstances to have a system with a non-zero $y_0$. Said second order differential equation
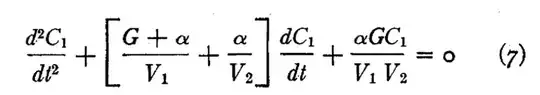 was used to model venous concentration following intravenous injection of exogenous creatinine in dogs, in a so-called two compartment model 1.
was used to model venous concentration following intravenous injection of exogenous creatinine in dogs, in a so-called two compartment model 1.
- $t_1$ is $\frac{1}{\ln2}$ times the "half-life" associated with the "first compartment" and $t_2$ is $\frac{1}{\ln2}$ times the so-called "terminal half-life." Actually, this is not exactly true as half-life of the plasma concentration is for all models, with the exception of a monoexponential, a function of time and not a collection of constants 2:
 Note that in the monoexponential case, and only in the monoexponential case, the equation above reduces to a constant half-life.
Note that in the monoexponential case, and only in the monoexponential case, the equation above reduces to a constant half-life.
- The so-called one-compartment model, or a monoexponential corresponds to the second OP question. It takes the form of the solution to a first order differential equation:$$\frac{dC(t)}{dt}=-k\;C(t)\;\;,$$
where $C(t)$ is a monoexponential model of venous concentration subsequent to a bolus venous injection. Again, this is not actually true for injected substances in organisms as the samples are drawn remote to the injection site, such that the initial concentration at $t=0$ is not a maximum value, but is actually zero. This model, and the "second order" one above, would more accurately describe one or two leaky gas cylinders whose internal pressures equilibrate much more quickly than they leak to each other or to an external vacuum. Similar to the above, the name "first order" is inherited from the "first order" differential equation.
1.) Sapirstein, L. A.; Vidt, D. G.; Mandel, M. J. & Hanusek, G. Volumes of distribution and clearances of intravenously injected creatinine in the dog. American Journal of Physiology. 1955, 181, 330-336
2.) Wesolowski, C. A.; Wesolowski, M. J.; Babyn, P. S. & Wanasundara, S. N.
Time varying apparent volume of distribution and drug half-lives following intravenous bolus injections. PLoS ONE, (2016), 11, e0158798