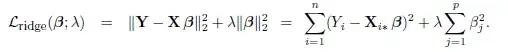My class started learning about ridge regression two weeks ago. Before that we learned about Lagrange multipliers and the connection between that and ridge penalty/constrain function.
Ridge:
Lagrange:
My question is why is the constant $c$ is not shown in ridge regression? Are we setting $c=0$? So is our constrain in ridge regression to set the sum of $\beta_j^2$ to zero?
Also, since $\beta_j^2$ is positive doesn't that mean that we are requiring all $\beta_j$ to equal to zero?