What is sigma function in the YOLO object detector?

Question

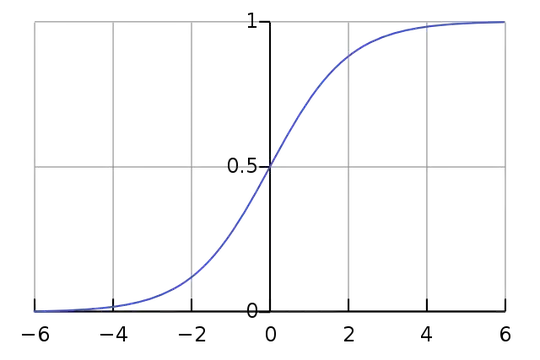
I have gone through the YOLO9000 paper, in that they have mentioned that network predicts 5 coordinates of the bounding box, and from that we find the exact centre coordinates and the width and height. I'm confused with those equations.
\begin{align} b_x &= \sigma(t_x) + c_x \\[3pt] b_y &= \sigma(t_y) + c_y \\[3pt] b_w &= p_we^{t_w} \\[3pt] b_h &= p_he^{t_h} \\[3pt] Pr({\rm object})\times IOU(b, {\rm object}) &= \sigma(t_o) \end{align}

In these equations, what does $\sigma$ stand for? Why they are using exponential for width and height?

Answer 1

It is the logistic sigmoid function: $$ \sigma(x) = \frac 1 {1+e^{-x}} $$ It is bounded between 0 and 1, which is a desired property in their case (image from Wikipedia):

Regarding the exponential, see this answer.

Answer 2

In addition to the notation using the symbol $\sigma$, the caption to one image names this function the "sigmoid" function. From the paper,

Figure 3: Bounding boxes with dimension priors and location prediction. We predict the width and height of the box as offsets from cluster centroids. We predict the center coordinates of the box relative to the location of filter application using a sigmoid function.

The "sigmoid" function is one of many names for a certain function. This name is especially common in the neural networks literature; for some elaboration, see Does the function $e^x/(1+e^x)$ have a standard name?