I'm working with a large set of accelerometer data collected with multiple sensors worn by many subjects. Unfortunately, nobody here seems to know the technical specifications of the devices and I don't think they have ever been recalibrated. I don't have a whole lot of info about the devices. I'm working on my master's thesis, the accelerometers were borrowed from another university and altogether the situation was a bit intransparent. So, preprocessing on-board the device? No clue.
What I do know is that they are triaxial accelerometers with a 20Hz sampling rate; digital and presumably MEMS. I'm interested in nonverbal behavior and gesturing, which according to my sources should mostly produce activity in the 0.3-3.5Hz range.
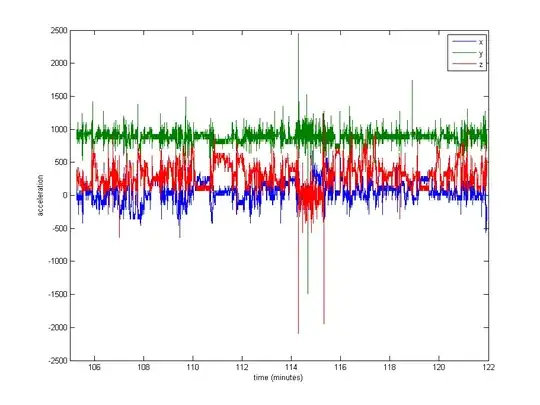
Normalizing the data seems quite necessary, but I'm not sure what to use. A very large portion of the data is close to the rest values (raw values of ~1000, from gravity), but there are some extremes like up to 8000 in some logs, or even 29000 in others. See the image below. I think this makes it a bad idea to divide by the max or stdev to normalize.
What's the usual approach in a case like this? Divide by the median? A percentile value? Something else?
As a side issue, I'm also not sure if I should clip the extreme values..
Thanks for any advice!
Edit: Here is a plot of about 16 minutes of data (20000 samples), to give you an idea of how the data is typically distributed.