@Ben provides most of the solution, here's a summary that fixes a minor error:
The sequence we are interested in consists of N monotonic elements ($X_1 < X_2 < ... < X_N$) followed by a non-monotonic element at position N+1. We are interested in $p(X_{N+1}=x)$
The PDF for the length of the monotonic sequence at the start of the chain (excluding the first non-monotonic sample) is $p(N=n) = \frac{n}{(n+1)!}$
The PDF for the maximum value among the first N+1 elements (which, in this context, is also the value of the element at position N) is $p(X_n=r | N=n) = (n+1)g(r)G(r)^n$, where G is the cumulative distribution function corresponding to g.
The distribution for $X_{N+1}$ is $p(X_{N+1} = x) = \sum_{n=1}^{\infty}\int_x^{\infty}{p(X_{N+1}=x|X_N=r, N=n)p(X_n=r|N=n)p(N=n)dr}$
Using the fact that $X_{N+1} < X_{N}$, the first term is equivalent to
$\sum_{n=1}^{\infty}\int_x^{\infty}{p(X_{N+1}=x|X_{N+1} < r, N=n)p(X_n=r|N=n)p(N=n)dr}$
Which we can flip around using Bayes' rule:
$\sum_{n=1}^{\infty}\int_x^{\infty}{\frac{p(X_{N+1}<r|X_{N+1}=x, N=n)p(X_{N+1}=x|N=n)}{p(X_{N+1} < r | N=n)}p(X_n=r|N=n)p(N=n)dr}$
Finally, plugging in $g$ and $G$ based on the above identities:
$ \sum_{n=1}^{\infty}\int_x^{\infty} \frac{g(x)}{G(r)}(n+1)g(r)G(r)^n\frac{n}{(n+1)!} dr$
$ \sum_{n=1}^{\infty}g(x)\frac{1}{n!}\int_x^{\infty}ng(r)G(r)^{n-1} dr$
$ \sum_{n=1}^{\infty}\frac{g(x)}{n!}[1 - G(x)^n]$
For the case where $X \sim U(0,1)$, $g(x)=1$, $G(x)=x$, and
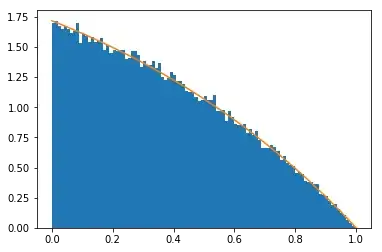
$p(X_{N+1})=\sum_{n=1}^{\infty}\frac{1-x^n}{n!} = e-e^x$
Which we can confirm against Monte Carlo simulation:
def sample(g = np.random.uniform):
x = top = g()
while x >= top:
top = x
x = g()
return x
def f(x):
return np.e - np.exp(x)
plt.hist([sample() for _ in range(100000)], bins=100, density=True)
x = np.linspace(0, 1, 20)
y = np.array([f(xx) for xx in x])
plt.plot(x, y)