Why is Gausian better then Quasi Poisson on the validation set while not on trainingset?

Question

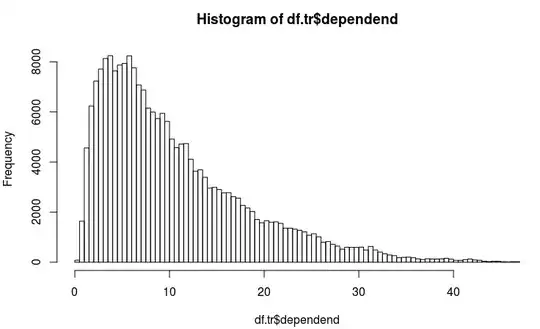
So we have a regression challenge here in which the dependent variable looks like this:

It is overdispersed as mean = 10 and variance = 60 so we think quasi-poisson is best?

We use the glm() functions in R.

We tried all of the below alternatives

m1g <- glm(round(dependend) ~ x1 * x2, data = df.tr )
m1g1 <- glm(dependend ~ x1 * x2, data = df.tr )
m1p <- glm(round(dependend) ~ x1 * x2, data = df.tr, family = "poisson" )
m1qp <- glm(round(dependend) ~ x1 * x2, data = df.tr, family = "quasipoisson" )
m1l <- glm(log(dependend) ~ x1 * x2, data = df.tr )

The dependend variable obviously is not normally distributed, also the lognormal is not optimal so we think quasi poisson should be best.

On the training set the residuals for the quasi poisson are a lot better the the gaussian model.

But we cant seem to beat the gaussian model on a validation set.

How can this be the case? Or what are we missing?

Model summary:

GAUSSIAN

> summary(m1g)

Call:
glm(formula = y ~ x1 * x2, data = df.tr)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-24.663   -2.849   -1.103    1.680   36.852  

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.5072026  0.0841578  41.674  < 2e-16 ***
x123        -2.2156110  0.2531252  -8.753  < 2e-16 ***
x124         0.2242957  0.1762014   1.273 0.203037    
x125         1.8011048  0.1166589  15.439  < 2e-16 ***
x126        -0.0409214  0.1239042  -0.330 0.741199    
x127         0.8896270  0.1363625   6.524 6.86e-11 ***
x128        -0.2410489  0.1604645  -1.502 0.133048    
x129         0.2261857  0.2166130   1.044 0.296397    
x137         3.3886973  0.3267226  10.372  < 2e-16 ***
x139        -2.4271957  0.2900612  -8.368  < 2e-16 ***
x140        -0.6184697  0.1820797  -3.397 0.000682 ***
x143        -1.6911565  0.3578242  -4.726 2.29e-06 ***
x146        -1.8280841  0.1685329 -10.847  < 2e-16 ***
x147         0.3685382  0.1221236   3.018 0.002547 ** 
x148         1.1061975  0.1372421   8.060 7.66e-16 ***
x149        -0.0386354  0.1523535  -0.254 0.799812    
x150         2.3230544  0.1218802  19.060  < 2e-16 ***
x151         1.3391181  0.1195007  11.206  < 2e-16 ***
x154         0.9155074  0.1156130   7.919 2.41e-15 ***
x155        -0.4611950  0.1148722  -4.015 5.95e-05 ***
x156        -0.1067856  0.1132884  -0.943 0.345887    
x157        -0.8609612  0.1216078  -7.080 1.45e-12 ***
x158        -0.6485214  0.1169027  -5.548 2.90e-08 ***
x159        -0.1946808  0.1168510  -1.666 0.095703 .  
x160         2.2581502  0.1283607  17.592  < 2e-16 ***
x190        -1.5436128  0.1248215 -12.367  < 2e-16 ***
x191         0.6596575  0.1149799   5.737 9.64e-09 ***
x192         0.1359673  0.1135766   1.197 0.231253    
x193        -0.1363663  0.1159813  -1.176 0.239692    
x194         0.5937715  0.1136418   5.225 1.74e-07 ***
x195        -0.7601841  0.1283618  -5.922 3.18e-09 ***
x196        -1.3666622  0.1251636 -10.919  < 2e-16 ***
x197         0.2268601  0.1251627   1.813 0.069907 .  
x2           0.0438423  0.0005247  83.564  < 2e-16 ***
x123:x2      0.0125207  0.0021183   5.911 3.41e-09 ***
x124:x2      0.0059799  0.0014012   4.268 1.98e-05 ***
x125:x2     -0.0051185  0.0006655  -7.692 1.46e-14 ***
x126:x2      0.0020976  0.0007717   2.718 0.006568 ** 
x127:x2     -0.0016735  0.0009182  -1.823 0.068367 .  
x128:x2     -0.0003740  0.0012000  -0.312 0.755268    
x129:x2      0.0045784  0.0019535   2.344 0.019096 *  
x137:x2     -0.0161315  0.0017495  -9.220  < 2e-16 ***
x139:x2      0.0325676  0.0039780   8.187 2.69e-16 ***
x140:x2      0.0007374  0.0016545   0.446 0.655808    
x143:x2     -0.0071728  0.0044617  -1.608 0.107917    
x146:x2      0.0115894  0.0012681   9.139  < 2e-16 ***
x147:x2      0.0049920  0.0007561   6.602 4.06e-11 ***
x148:x2      0.0007417  0.0008443   0.879 0.379668    
x149:x2      0.0159149  0.0008658  18.383  < 2e-16 ***
x150:x2     -0.0011305  0.0006279  -1.800 0.071813 .  
x151:x2     -0.0018370  0.0006683  -2.749 0.005980 ** 
x154:x2     -0.0090907  0.0007118 -12.771  < 2e-16 ***
x155:x2     -0.0025856  0.0006574  -3.933 8.38e-05 ***
x156:x2     -0.0064424  0.0006228 -10.344  < 2e-16 ***
x157:x2      0.0022582  0.0006704   3.368 0.000756 ***
x158:x2     -0.0012893  0.0006624  -1.946 0.051619 .  
x159:x2     -0.0029377  0.0006449  -4.555 5.24e-06 ***
x160:x2     -0.0027016  0.0006721  -4.020 5.82e-05 ***
x190:x2      0.0070651  0.0007176   9.845  < 2e-16 ***
x191:x2      0.0039843  0.0006248   6.377 1.81e-10 ***
x192:x2      0.0007105  0.0006126   1.160 0.246164    
x193:x2      0.0053882  0.0006294   8.561  < 2e-16 ***
x194:x2      0.0092873  0.0006285  14.777  < 2e-16 ***
x195:x2      0.0068949  0.0007203   9.572  < 2e-16 ***
x196:x2      0.0211705  0.0006963  30.402  < 2e-16 ***
x197:x2      0.0085271  0.0007383  11.550  < 2e-16 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for gaussian family taken to be 24.77175)

    Null deviance: 13114523  on 217221  degrees of freedom
Residual deviance:  5379335  on 217156  degrees of freedom
AIC: 1313736

Number of Fisher Scoring iterations: 2

QUASI POISSON

> summary(m1qp)

Call:
glm(formula = y ~ x1 * x2, family = "quasipoisson", data = df.tr)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-7.1160  -1.1881  -0.3811   0.6225   8.5814  

Coefficients:
              Estimate Std. Error t value Pr(>|t|)    
(Intercept)  1.620e+00  1.021e-02 158.706  < 2e-16 ***
x123        -5.363e-01  3.787e-02 -14.160  < 2e-16 ***
x124        -2.613e-02  2.186e-02  -1.195 0.232091    
x125         3.103e-01  1.335e-02  23.245  < 2e-16 ***
x126         4.703e-03  1.505e-02   0.312 0.754671    
x127         9.312e-02  1.637e-02   5.689 1.28e-08 ***
x128        -9.756e-02  2.004e-02  -4.867 1.13e-06 ***
x129        -5.968e-02  2.739e-02  -2.179 0.029366 *  
x137         3.954e-01  3.645e-02  10.847  < 2e-16 ***
x139        -7.190e-01  4.710e-02 -15.266  < 2e-16 ***
x140        -3.025e-01  2.572e-02 -11.759  < 2e-16 ***
x143        -7.921e-01  6.613e-02 -11.977  < 2e-16 ***
x146        -4.221e-01  2.343e-02 -18.012  < 2e-16 ***
x147         8.399e-02  1.460e-02   5.754 8.72e-09 ***
x148         1.914e-01  1.596e-02  11.995  < 2e-16 ***
x149         1.806e-01  1.723e-02  10.477  < 2e-16 ***
x150         4.901e-01  1.326e-02  36.947  < 2e-16 ***
x151         2.632e-01  1.371e-02  19.192  < 2e-16 ***
x154         7.562e-02  1.403e-02   5.388 7.13e-08 ***
x155        -5.266e-02  1.409e-02  -3.738 0.000186 ***
x156         1.221e-03  1.384e-02   0.088 0.929705    
x157        -2.899e-02  1.459e-02  -1.987 0.046921 *  
x158        -5.871e-02  1.426e-02  -4.118 3.82e-05 ***
x159         3.489e-02  1.400e-02   2.492 0.012706 *  
x160         3.945e-01  1.430e-02  27.577  < 2e-16 ***
x190        -1.491e-01  1.547e-02  -9.635  < 2e-16 ***
x191         3.375e-01  1.287e-02  26.220  < 2e-16 ***
x192         1.980e-01  1.316e-02  15.040  < 2e-16 ***
x193         2.456e-01  1.307e-02  18.785  < 2e-16 ***
x194         3.872e-01  1.257e-02  30.813  < 2e-16 ***
x195        -1.913e-02  1.559e-02  -1.227 0.219708    
x196         8.074e-02  1.446e-02   5.584 2.36e-08 ***
x197         1.808e-01  1.430e-02  12.644  < 2e-16 ***
x2           3.896e-03  4.775e-05  81.584  < 2e-16 ***
x123:x2      2.894e-03  2.228e-04  12.986  < 2e-16 ***
x124:x2      1.056e-03  1.363e-04   7.746 9.50e-15 ***
x125:x2     -1.201e-03  5.768e-05 -20.823  < 2e-16 ***
x126:x2      7.827e-05  6.976e-05   1.122 0.261896    
x127:x2     -2.167e-05  8.574e-05  -0.253 0.800490    
x128:x2      4.151e-04  1.111e-04   3.736 0.000187 ***
x129:x2      1.283e-03  1.974e-04   6.497 8.23e-11 ***
x137:x2     -1.570e-03  1.652e-04  -9.505  < 2e-16 ***
x139:x2      7.379e-03  4.674e-04  15.787  < 2e-16 ***
x140:x2      1.995e-03  1.870e-04  10.667  < 2e-16 ***
x143:x2      4.490e-03  7.130e-04   6.297 3.03e-10 ***
x146:x2      2.632e-03  1.355e-04  19.427  < 2e-16 ***
x147:x2      1.392e-04  6.840e-05   2.036 0.041782 *  
x148:x2     -4.827e-04  7.295e-05  -6.618 3.66e-11 ***
x149:x2     -2.145e-05  7.155e-05  -0.300 0.764367    
x150:x2     -1.617e-03  5.328e-05 -30.347  < 2e-16 ***
x151:x2     -8.422e-04  5.930e-05 -14.202  < 2e-16 ***
x154:x2     -5.533e-04  6.708e-05  -8.249  < 2e-16 ***
x155:x2     -2.465e-04  6.040e-05  -4.081 4.48e-05 ***
x156:x2     -6.778e-04  5.719e-05 -11.852  < 2e-16 ***
x157:x2     -1.099e-04  6.114e-05  -1.797 0.072403 .  
x158:x2     -1.491e-04  6.112e-05  -2.439 0.014727 *  
x159:x2     -5.313e-04  5.873e-05  -9.047  < 2e-16 ***
x160:x2     -1.210e-03  5.871e-05 -20.613  < 2e-16 ***
x190:x2      3.115e-04  6.433e-05   4.842 1.28e-06 ***
x191:x2     -1.283e-03  5.282e-05 -24.281  < 2e-16 ***
x192:x2     -1.045e-03  5.344e-05 -19.559  < 2e-16 ***
x193:x2     -1.033e-03  5.350e-05 -19.309  < 2e-16 ***
x194:x2     -1.242e-03  5.235e-05 -23.719  < 2e-16 ***
x195:x2      7.185e-05  6.448e-05   1.114 0.265129    
x196:x2      2.888e-04  5.990e-05   4.821 1.43e-06 ***
x197:x2     -3.369e-04  6.226e-05  -5.411 6.29e-08 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for quasipoisson family taken to be 2.80759)

    Null deviance: 1145349  on 217221  degrees of freedom
Residual deviance:  538764  on 217156  degrees of freedom
AIC: NA

Number of Fisher Scoring iterations: 5

Unfortunately, the distribution of the response tells you little about what form of regression might be appropriate. For *all* regression problems you need to characterize the *conditoinal* distributions of the response. If you could illustrate those, we might be able to provide more help. — whuber, Apr 09 '19 at 13:17
Hi @whuber thx for your response ,can you elaborate a bit what you mean? The dependend variable is the number of hours I have to wait before an event occurs... On the training dataset the quasi-poisson model has smaller residual(as can be seens in the summaries, not all factors are sigificant but the model structure is for both models the same, only the family differs. On the validation set the gaussian is better the the poisson, so is the quasi-poisson overfit? How can I tell ? I expect the quasi poisson to also do better on the validation set... — Hugo Koopmans, Apr 09 '19 at 15:14

score 0 · Answer 1 · answered Apr 09 '19 at 15:26

You cannot determine the shape of the distribution of a GLM response by looking at an unconditional histogram. You haven't accounted for the impact of the regressors. Instead, bin sets of regressors and look at a panels of histograms with superimposed density lines for the best fitting Poisson distribution in that analysis set, using MLE.
"Statistical significance" is not really a basis for "doing better". One set of models could have a high false positive error rate and an uncontrolled type 1 error rate. I would look at the MSE of predicted response in the validation set.
You rounded the response to fit a Poisson regression why? Despite R's warnings you do not in fact need to round a response to fit a Poisson GLM. If you round the response, you lose precision. See my answer here about conditions for using Poisson GLMs.
The whole purpose of having a testing validation set is to have a final say as to which model is better. A model which overfits in the training set will do worse in the validation set.

Why is Gausian better then Quasi Poisson on the validation set while not on trainingset?

1 Answers1