1

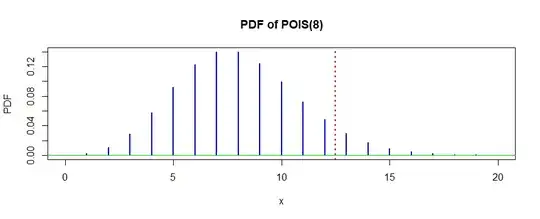
The situation I have is with data that (I'm assuming for now) follows a poisson distribution. I want to know if this year had an unusual number of a certain type of fatality compared to previous years. I could use a hypothesis test to evaluate if this result is unusual. If the average rate in previous years was 8 fatalities per year, and last year there were 13 fatalities:

Null hypothesis: λ = 8 Alternative hypothesis: λ > 8 Using a cumulative poisson distribution table, I can see that P[x>=13] = 0.0342 when λ = 8 is, so the result is statistically significant at the 0.05 level.

However, I only have a few years of data with which to estimate my null hypothesis λ = 8. I know that the standard error for my estimate is sqrt(λ/n) - how do I include this extra uncertainty in my hypothesis test?

Thanks!

Edit: Thanks everyone for your responses so far. Some have asked for specifics of the data I am looking at. I actually want to stay away from solutions for specific data since this is a business question that comes up a lot in with different types of accidents and with different numbers of years available, and I'm looking for a good general solution. If it helps, lets say I always have between 7 and 15 years of data to give me my null hypothesis lambda.

KDford
  • 11
  • 2

2 Answers2

0

This is a difficult situation with not much data, but I think your analysis is reasonable. However, it seems you have a computational error.

Suppose $40$ accidents of a particular kind over the last $5$ years. (The annual numbers may have been 7. 11, 5, 9, 8.) It seems reasonable to model these accidents according to a Poisson distribution and the estimated Poisson mean is $\hat \lambda = 40/5 = 8.$

Now in the current year just finished, there have been $13$ accidents of this kind. It is certainly possible that one of the previous five years might have had $13$ accidents. The annual numbers might have been 7, 8, 13, 9, 3. Generally speaking, it is certainly possible for a Poisson distribution to produce an occasional large count.

How likely is that? The result from R is $P(X \ge 13) = 1 - P(X \le 12) = 0.064.$ So the P-value of your test is about 6.4% > 5% and you cannot reject $H_0: \lambda = 8$ in favor of $H_a: \lambda > 8$ at the 5% level of significance.

1 - ppois(12, 8)
[1] 0.0637972

enter image description here

If the count for the most recent year had been $14$ then the P-value would be about 3.4%, leading to rejection at the 5% level.

1 - ppois(13, 8)
[1] 0.0341807

Notes: With so little data and with 'borderline' P-values, subjective factors are bound to affect the believability of this test:

(a) In order for this test procedure to work, it is necessary for the correct model to be Poisson with the same mean $\lambda$ holding true throughout the 5-year reference period. With only five years of data for reference, there is no way to check whether the Poisson model is correct or whether $\lambda$ has been constant.

If the numbers for the past five years were something like 5, 7, 9, 8, 11, then I would worry that there might be an increasing accident rate across all six years. In that case it wouldn't be surprising for the sixth year to be larger.

(b) If something occurred just before the beginning of the last year (with its 13 accidents) that might be expected to increase the accident rate, and that occurrence triggered doing the test, then I would be more inclined to trust the test. (E.g., heavier traffic on a road due to a new factory nearby, or major construction with narrower traffic lanes at unpredictable places throughout the year.)

By contrast, if you just notice a year with 13 accidents and decide to do a test based on that alone, I would be less inclined to trust the test.

BruceET
  • 47,896
  • 2
  • 28
  • 76
  • Although your *caveats* are well considered, I believe they don't validate your approach. Any comparison of this year's result to the previous years' results ought to handle the uncertainties in all six years of data appropriately, rather than assuming there is no uncertainty in the first five. Thus, given there is an unknown underlying distribution common to all *six* years, what evidence against this does the value $(40,13)$ of the random variable $(X,Y)$ given by the sum of five years and the sixth year provide? Using $Y-X/5$ as test statistic, $p\approx 11.5\%$ isn't significant. – whuber Mar 31 '19 at 22:23
  • Another way to look at this is to examine the distribution of the largest value out of six independent draws from a Poisson$((40+13)/6)$ distribution: $13$ is its median value! (The chance of $13$ or larger is $51\%.$) Thus, we should *expect* to see a value of $13$ in six years. Even the appearance of the $13$ in a specific year of interest (the latest) is still no real surprise. – whuber Mar 31 '19 at 22:28
  • @whuber: OP said 'previous years' and I think it was a bad idea to take that to be 5. I understand the argument about looking at the max. However, I'm confused about median of POIS(53/6) being 13: from `qpois(.5, 53/6)` I get 9. Anyhow, it seems neither of the two Answers works well, and I'm willing to delete mine. Do you think there is _any_ good Answer to the original question? – BruceET Apr 01 '19 at 00:10
  • The median of the *maximum* of six iid observations is 13. – whuber Apr 01 '19 at 03:24
  • @whuber your first comment gets at exactly my problem: all examples I see of hypothesis tests use some "known" value of lambda - but I don't have much confidence in the only value for lambda I have available, which is the average for the past 7-15 years. – KDford Apr 01 '19 at 14:19
  • I wonder if there is a way to brute force this. If I calculate a confidence interval for my lambda, and then use the upper bound of the 95% CI as the null hypothesis lambda, and my value for last year still has p <= 0.05 using that test, then clearly last year's result would be a significant change. However, the "real"/total P-value of the upper p=0.05 limit of that hypothesis test would really be the upper limit of the 95% CI (p=0.025) x the &alpha of my hypothesis test (0.05) = 0.0125. – KDford Apr 01 '19 at 14:54
  • Would it then make sense to write a script to conduct hypotheses tests on each value of lambda in the 95% CI, starting at the upper limit and working its way down to my observed average, until I end up with a value where (the p-value based on the probability distribution of my observed lambda) * (the probability of of my "last year" value) <0.05? I'm struggling with how to word this so apologies if that's not clear – KDford Apr 01 '19 at 15:09
  • It would help if you could give actual data for the 'previous years' providing the estimate $\hat \lambda = 8.$ How many years and why you think $\lambda$ has been constant during that period. Also, has there been some change that leads you to suspect that the true $\lambda$ may have increased? If your only reason to suspect a change is seeing 13 accidents in the yr immediately previous, then a different approach may be needed. Poisson dist'ns have no cap on the possible nr of accidents and occasional high values are to be expected: among $10^6$ samples of size 10 from POIS(8) 4% had max > 16. – BruceET Apr 01 '19 at 17:56
  • Thanks @BruceET. I made an edit to my original post to mention that I'm looking for a general solution to this problem, not just a solution for this particular data. You make a good point that higher values are to be expected with poisson distributions, and in fact a big reason that I am looking to a statistical approach to reassure management that occasional blips like this are not necessarily big warning signs that things are getting worse. – KDford Apr 01 '19 at 18:08
  • @whuber I like your approach of looking at the distribution of the largest values in a simulation, but I'm not sure if using a Poisson((40+13)/6 distribution (i.e. including the year that is potentially abnormal, lets call it year 6) gets me closer to evaluating whether year 6 represents a change from prior years. Repeating the same process with Poisson((40)/5) is closer to what I want to check (gives me 32% of 6 independent draws with a value >= 13), but I don't think this helps with trying to capture the uncertainty around the lambda itself. – KDford Apr 01 '19 at 18:53
  • It is useful to adopt, as a null hypothesis, that there has been no change in the distribution. In that case the best estimate of the Poisson parameter is obtained by using all six years of data, not just the first five: that's why (40+13)/6 is the right value to use. It's also possible--and, I believe, nearly equivalent (although more complicated to work out)--to use the first five years of data to construct a prediction interval for the sixth year. – whuber Apr 03 '19 at 14:22
-1

My first-nanosecond, Malcolm-Gladwell-Blink-level reaction asks why you're using the cumulative Poisson as the distribution of your test statistic. If you've got a small number of samples from any distribution (including the Poisson), the Central Limit Theorem says you can use the t- or F- distribution (via a t-test or an ANOVA) to test your hypothesis. The small sample size would be worked into your test in computing the degrees of freedom.

So, H0: λ = 8, HA: λ ≠ 0, and since you have a small sample ("a few data points"), compute a t-statistic with df = a few − 1.

If there's a reason to use a Poisson CDF, I'm not seeing it at the moment. Tell us more, or give us more data or more context.

Sciolism Apparently
  • 111
  • 5
  • 1
    Could you please explain how the CLT might apply to a "small number of samples" from "any distribution"? Both quoted phrases appear to *preclude* application of the CLT. – whuber Mar 31 '19 at 22:13
  • You’re absolutely right about “a few”. It depends on the underlying distribution. I don’t know how many data points he has, and tried to qualify it. The CLT is powerful, so without looking at the data, I couldn’t say specifically. There are always nonparametric/distribution free methods available. If the original poster followed up, that would have been my next suggestion. – Sciolism Apparently Mar 31 '19 at 22:26
  • @whuber Also, the CLT says that any—really, any—original distribution, will produce sample distributions that approach normality. I feel sure you know how to do a simulation: start with something completely non-normal, like, say, a Chi-Squared distribution with 1df. Randomly sample 5 values, average them, and plot the average. Do the same thing again. And again. By the time you’re around 20–30, the sampling distribution will look Normal. My point was that I couldn’t imagine using Poisson as the distribution of a sampling stat. – Sciolism Apparently Mar 31 '19 at 22:37
  • Please see https://stats.stackexchange.com/questions/69898/t-test-on-highly-skewed-data for one (real world) reason why your assertions are not true. In the present case, since there is exactly *one* observation in year 6, the CLT is utterly silent about how it might reasonably be compared to the sum for years 1-5. – whuber Mar 31 '19 at 22:40
  • @whuber The only information that existed in the thread when I responded was that the original data followed a Poisson distribution, with an average of 8 fatalities for an unknown number of years, and that last year there were 13 fatalities. How many are in each year I have no idea. Certainly, years with zero or one data point are special cases. But that kind of specificity wasn’t present in the original question or my response. Note my final sentence asking for more info, more data, more context. – Sciolism Apparently Mar 31 '19 at 23:13
  • If you need more information to answer a question, then please ask for it in a comment, rather than a response. Note that the question has not (yet) been edited. – whuber Apr 01 '19 at 03:24
  • @whuber That was my first instinct as well, to add a comment, and I tried. However, I’ve only just joined the group and haven’t accumulated enough points to add a comment yet. So, I gave a response that proposed an answer under likely yet general conditions, and asked for more specificity to see if those conditions were correct. I agree that the question hasn’t been edited yet...does that imply something I’m not seeing? I was the first to respond to a question that is exactly as it is now. I’m hoping we’ve all helped the original poster. – Sciolism Apparently Apr 01 '19 at 03:53