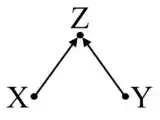
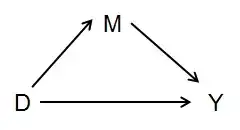
There are various matching procedures in the causal inference literature, from exact matching to propensity score matching and more. The goal is usually to find the Average Treatment Effect (ATE). Most literature seem to encourage the researcher to add as many covariates as they can that they think would influence the outcomes. This is to reduce the confounding bias.
However, I am wondering if there are cases where matching on more covariates would result in more bias. In other words, are there scenarios where removing covariates to match on gives a better estimate of the ATE? Thanks.