Why does larger perplexity tend to produce clearer clusters in t-SNE?

Question

Why does larger perplexity tend to produce clearer clusters in t-SNE?

By reading the original paper, I learned that the perplexity in t-SNE is $2$ to the power of Shannon entropy of the conditional distribution induced by a data point. And it is mentioned in the paper that it can be interpreted as a smooth measure of the effective number of neighbors.

If the conditional distribution of a data point is constructed by Gaussian distribution (SNE), then the larger the variance $\sigma^2$, the larger the Shannon entropy, and thus the larger the perplexity.

So, the intuition that I built is:

The larger the perplexity, the more non-local information will be retained in the dimensionality reduction result.

When I use t-SNE on two of mine test datasets for dimensionality reduction, I observe that the clusters found by t-SNE will become consistently more well-defined with the increase of perplexity. Although this is a desirable outcome, I just cannot explain this with the intuition that I just built.

Here is the result that I have, the data and the script used for generating the figure have been uploaded here:

Besides the confusion that I just mentioned, I also don't know how to interpret the result.

What could be a possible explanation for the fact that it is easier for t-SNE to find well-defined clusters in Random dataset then Benchmark dataset?

Answer 1

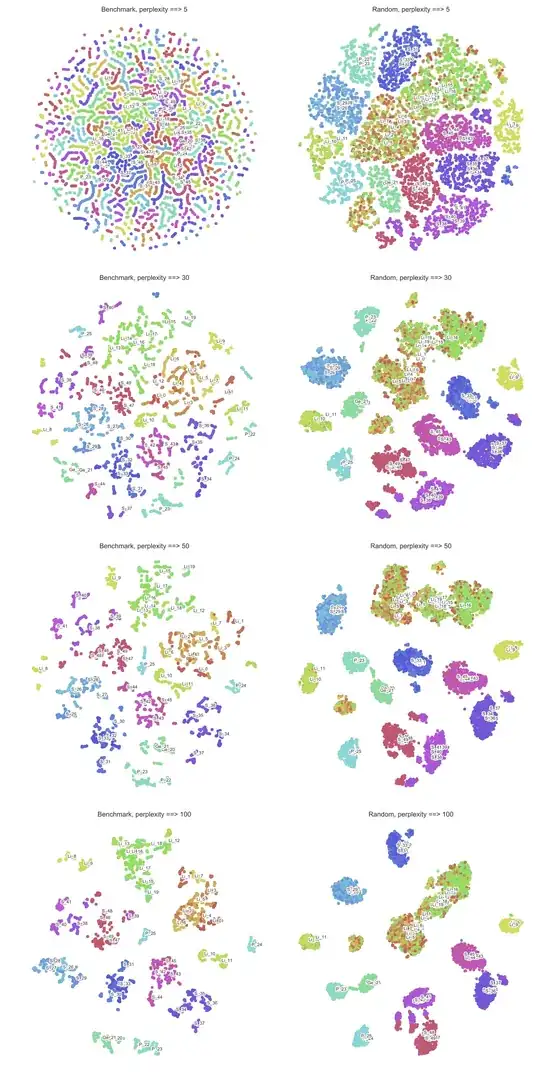
The larger the perplexity, the more non-local information will be retained in the dimensionality reduction result.

Yes, I believe that this is a correct intuition. The way I think about perplexity parameter in t-SNE is that it sets the effective number of neighbours that each point is attracted to. In t-SNE optimisation, all pairs of points are repulsed from each other, but only a small number of pairs feel attractive forces.

So if your perplexity is very small, then there will be fewer pairs that feel any attraction and the resulting embedding will tend to be "fluffy": repulsive forces will dominate and will inflate the whole embedding to a bubble-like round shape.

On the other hand, if your perplexity is large, clusters will tend to shrink into denser structures.

This is a very handway explanation and I must say that I have never seen a good mathematical analysis of this phenomenon (I suspect such an analysis would be nontrivial), but I think it's roughly correct.

---

It is instructive to see it in a simulation. Here I generated a dataset with six 10-dimensional Gaussian balls ($n=1000$ in each ball) that are located very far away from each other --- so far that even for perplexity 100 all attractive forces are within-cluster. So for perplexities between 5 and 100, shown below, there are never any attractive forces between clusters. However, one can clearly see that the clusters "shrink" when perplexity grows.

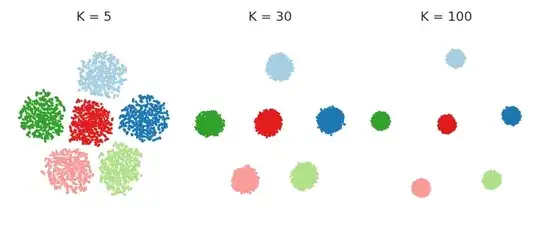
In fact, one can get rid of perplexity entirely, and make each point feel equally strong attraction to its closest $K$ neighbours. This means that I replace the Gaussian kernel in the high-dimensional space with the "uniform" kernel over the closest $K$ neighbours. This should simplify any mathematical analysis and is arguably more intuitive. People are often surprised to see that the result very often looks very similar to the real t-SNE. Here it is for various values of $K$:

---

Code

%matplotlib notebook

import numpy as np
import pylab as plt
import seaborn as sns

sns.set_style('ticks')

# https://github.com/KlugerLab/FIt-SNE
import sys; sys.path.append('/home/localadmin/github/FIt-SNE')
from fast_tsne import fast_tsne

col = np.array(['#a6cee3','#1f78b4','#b2df8a','#33a02c','#fb9a99',
                '#e31a1c','#fdbf6f','#ff7f00','#cab2d6','#6a3d9a'])

n = 1000  # sample size per class
p = 10    # dimensionality
k = 6     # number of classes
d = 10    # distance between each class mean and 0

np.random.seed(42)
X = np.random.randn(k*n, p)
for i in range(k):
    X[i*n:(i+1)*n, i] += d

perpl = [5, 30, 100]
Z1 = []
for p in perpl:
    Z = fast_tsne(X, perplexity=p, seed=42)
    Z1.append(Z)

ks = [5, 30, 100]
Z2 = []
for kk in ks:
    Z = fast_tsne(X, K=kk, sigma=10000, seed=42)
    Z2.append(Z)


fig = plt.figure(figsize=(7, 3))

for i,Z in enumerate(Z1):
    plt.subplot(1,3,i+1)
    plt.axis('equal', adjustable='box')
    plt.scatter(Z[:,0], Z[:,1], s=1, c=col[np.floor(np.arange(n*k)/n).astype(int)])
    plt.title('Perplexity {}'.format(perpl[i]))
    plt.gca().get_xaxis().set_visible(False)
    plt.gca().get_yaxis().set_visible(False)

sns.despine(left=True, bottom=True)
plt.tight_layout()


fig = plt.figure(figsize=(7, 3))

for i,Z in enumerate(Z2):
    plt.subplot(1,3,i+1)
    plt.axis('equal', adjustable='box')
    plt.scatter(Z[:,0], Z[:,1], s=1, c=col[np.floor(np.arange(n*k)/n).astype(int)])
    plt.title('K = {}'.format(perpl[i]))
    plt.gca().get_xaxis().set_visible(False)
    plt.gca().get_yaxis().set_visible(False)

sns.despine(left=True, bottom=True)
plt.tight_layout()

Answer 2

I believe this is because of this mismatch in t-SNE between the input (Gaussian) and output (student-t) distributions. It is beneficial to make such blobs in order to separate from everything else as required by the long tail of the t-distribution. The repulsive forces dominate.

In such cases SNE may work better. Have you tried?