compute sample probabilities given a poisson distribution

Question

I have read through a large number of stack posts about hypothesis testing on Poisson distributions. Some examples:

• Calculating test statistic of a poisson distribution
• Hypothesis testing with Poisson Data
• hypothesis testing using poisson distribution

The above four posts ask this question in slightly different ways, yet the answers obtained are not recognizably similar. Thus I will ask the question here in hopes of obtaining an authoritative answer.

The question

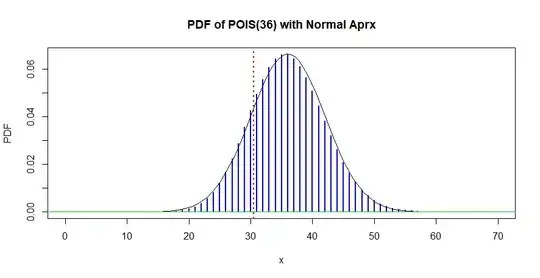
I have a Poisson distribution with known mean $\mu$. What is the probability of obtaining a single sample from that distribution which is greater than some value $x$?

Relatedly, what is the probability of drawing $n$ samples from that distribution which have an average value greater than $\bar{x} = \sum_i^n{x_i} / n$.?

Since the variance of the Poisson distribution is equal to its mean $\mu$, we may compute a Z-score like:

$$ z = \frac{x-\mu}{\sqrt{\mu}} $$

I have not seen this expressed explicitly anywhere, but I assume the generalization to multiple samples is accomplish like:

$$ z = \frac{\bar{x}-\mu}{\sqrt{\mu / n}} $$

With a Z-score in hand, one can look up the probability using the Z distribution CDF. In python:

import scipy.stats
p = scipy.stats.norm.cdf(z)

Firstly, I am wondering if the above characterization of the approach is correct. This is simply the understanding I have gleaned from searching the topic.

Secondly, where does this approach come from? For example, in the case of an academic paper, whom would I cite about such an approach?

Finally, the normal approximation is sometimes but not always mentioned in posts on this topic. Does the above approach use the normal approximation? As such, is it inappropriate for $\mu$ with smaller values? If so, what would be an appropriate test?

Answer 1

If random variable $X \sim \mathsf{Pois}(\lambda),$ then $E(X) = Var(X) = \lambda.$ The PDF is $p_k = P(X = k) = e^{-\lambda}\lambda^k/k!,$ for integer $k \ge 0.$ The CDF is $F_X(k) = P(X \le k) = \sum_{k=0}^x p_k$ and $P(X>k) = 1 - F_X(k).$

Example: If $X \sim \mathsf{Pois}(\lambda = 3),$ then $P(X = 4) = 01680,$ $P(X\le 4)=0.8153,$ $P(X > 4) = 0.1847$ according to the following computations in R:

lam = 3;  dpois(4, lam);  ppois(4, lam);  1 - ppois(4, lam)
[1] 0.1680314
[1] 0.8152632
[1] 0.1847368

If $X_1, X_2, \dots, X_n$ are a random sample from $\mathsf{Pois}(\lambda)$ and $\bar X = \frac{1}{n}\sum_{i=1} ^n X_i$ then $$n\bar X = \sum_{i=1}^n X_i \sim \mathsf{Pois}(n\lambda).$$

For $\lambda$ sufficiently large, both of your normal approximations may be useful.

Example: If $\lambda = 36$ then $P(X \le 30)=0.1806$ can be approximated by $P(X^\prime \le 30.5) = 0.1797,$ where $X^\prime \sim \mathsf{Norm}(\,u = 36,\, \sigma=6).$ Standardizing, the approximation is $$P(X \le 30) = P(X < 30.5) = P\left(\frac{X-\mu}{\sigma} < \frac{30.5-36}{6}\right)\\ \approx P(Z < -0.9167) = 0.1797,$$ where the value obtained from printed tables of the standard normal CDF, rounding to $-0.92,$ is a little different.

lam = 36;  ppois(30, 36) 
[1] 0.1806255
pnorm(30.5, 36, 6)
[1] 0.1796587
pnorm((30.5 - 36)/6)
[1] 0.1796587