0

This is part of a bigger quantitative reasoning assignment I was working on.

My understanding here is that the upper bound and lower bound of the ranges for each of the exercises should be reflected by the numbers in the brackets, but they are somewhat not drawn to scale. The black dot that is always placed conveniently in the middle of the bounds, has a magnitude given by the number outside the bracket, which is also the OR adjusted for confounders. The OR’s relative position to 1 is indicated in the same diagram.

A question I would like to ask is how is this range calculated? My thinking is that the 95% CI means +_0.05 to the mean value, which is the OR value, but that doesn’t get me the 2 bounds of the range. For some reason the OR = 1 also doesn’t lie in between the range of Dancing, and this is partly because all the exercises have different range sizes. This doesn't make sense to me since all of them have the same CI.

Can anyone explain this to me?

Stats image

Prashin Jeevaganth
  • 135
  • 5

1 Answers1

1

A confidence interval is an interval estimate of the population parameter. It is constructed in such a way that across many samples, it excludes the population parameter only with probability $\alpha$ (i.e., .05). If the value of the population parameter under the null hypothesis is outside the confidence interval, you can reject the null hypothesis. This is equivalent to finding a p-value less than $\alpha$.

Confidence intervals are constructed as $\hat{\theta}\pm 1.96 \times SE$, where $\hat{\theta}$ is the point estimate of the population parameter. 1.96 is the critical T-statistic for $\alpha=.05$ with a very large degrees of freedom (i.e., sample size). The standard error (SE) is a measure of the certainty of your estimate, and depends on the data and sample size.

Odds ratios are estimated using logistic regression. However, logistic regression actually estimates the log of the odds ratio. The standard error it estimates is the standard error of the log odds ratio, and the confidence interval is around the log odds ratio. This confidence interval is symmetric as the formula above implies. Log odds ratios are challenging to interpret, so to get to the odds ratio, you can just exponentiate (i.e., raise $e$ to the power of) the log odds ratio estimated from logistic regression. You can also exponentiate the bounds of the confidence interval for the log odds ratio. This yields the odds ratio and a confidence interval for the odds ratio. The confidence interval for the odds ratio is not symmetric even though the confidence interval for the log odds ratio is.

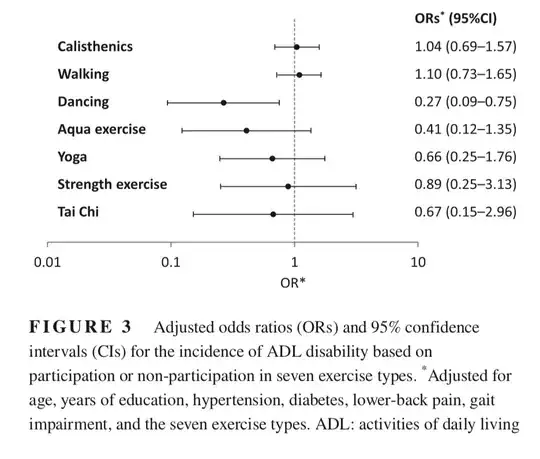
The graph plots the odds ratio of disability for each "treatment" variable. The black dot is the estimated odds ratio, and the bars are the confidence intervals around the odds ratio. What complicates this a bit is that the graph is displayed with a log-transformed x-axis. This is useful because an odds ratio of 10 and .1 represent the same size of effect (in opposite directions), so they should be equally far from 1 (i.e., which indicates no effect). To make such a graph, you simply take the log of the values on the x-axis. It's not that the points are plotted not to scale; its that the scale changes as you move from left to right.

Because we've taken the log of the x-axis, the confidence intervals for the odds ratio plotted on the log scale are symmetric because the confidence interval for the log odds ratio is symmetric, even though the confidence interval for the odds ratio on a standard scale is not symmetric.

The fact that the confidence interval for the odds ratio for Dancing excludes 1 means that dancing has a negative effect on disability (i.e., dancing decreases the odds of having an ADL disability). There is no evidence that any of the other exercise types affect the odds of having a disability because all of their confidence intervals contain 1.

Noah
  • 20,638
  • 2
  • 20
  • 58
  • Thanks for your answer, I think I understood that the axis labels and all the values on the chart must be logged to appreciate the symmetric property. However, I am still confused why the range would be different for each of the exercise types, since all of them have a confidence interval of 95%, which means the estimated mean +-0.05? – Prashin Jeevaganth Mar 27 '19 at 01:05
  • They aren't equal to the estimated mean $\pm$.05. I provided the formula for the CI in my answer. The SE differs for each exercise type, so the confidence interval widths will differ. The SE depends on how correlated the variable is with the other variables and what proportion of people did each exercise type. – Noah Mar 27 '19 at 01:31
  • Apparently the exercise types are arranged in descending order from top to down based on their proportion of people doing it, am I right to say "generally" speaking the SE decreases with increasing proportion because the random error component is being decreased. And the correlation with other variables(like the different exercise types and confounders) is also directly proportional to the SE? It seems to be the case for this but there are some exceptions in between. – Prashin Jeevaganth Mar 27 '19 at 01:45