1

I have some data samples , used histfit in matlab and did some integrated tests in matlab to test if the data is normally distributed, but i`m not convinced.

I have around 200 values in my sample

  • Can I tell from the graphs if it is nor not?
  • All my data has to be under the curve to be normally distributed?

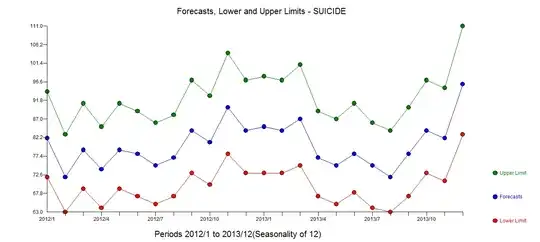
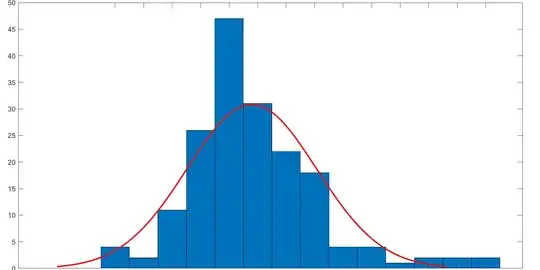
Pics related: Sample 1 Sample 2 Sample 3

random_numbers
  • 13
  • 4
  • What does your data actually represent? That might already give you an answer to your question w/o actually needing to "look at the data". – Georg M. Goerg Mar 26 '19 at 11:19
  • It represents execution times of a repetitive function, in nanoseconds. – random_numbers Mar 27 '19 at 19:29
  • Ok, so strictly speaking it can't be normal then since its strictly positive. For (waiting) times usually an exponential distribution is a good starting point. Or log normal if you want to keep normality around. – Georg M. Goerg Mar 28 '19 at 02:48

2 Answers2

2

Perfectly normally distributed data is in practice effectively non-existent. While one can manipulate bin widths to show many things or end up with misleading plots, your data does not look normal.

But why do you want to know? If you care about what analysis method to use, then firstly you should not care about the data (i.e. dependent and independent variables), but the regression residuals. Secondly, deviations don't necessarily invalidate a model with normally distributed error terms.

Nick Cox
  • 48,377
  • 8
  • 110
  • 156
Björn
  • 21,227
  • 2
  • 26
  • 65
1

All my data has to be under the curve to be normally distributed?

No, it doesn´t.

Can I tell from the graphs if it is nor not?

As you said yourself: i`m not convinced. To convince yourself one way, or another, you can either make another plot (like QQ-plot), or do a statistical test for normality and check if the p-value is significant. Shapiro-wilk test is quite common though it seems that directed tests assessing skewness or curtosis should be preferred. It all depends on what you are planning to do in the next step. Student´s t test is more sensitive to skewness, while tests with inference about variances might be sensitive to kurtosis.

Oka
  • 523
  • 2
  • 6