2

I want to generate 500 simulations of my original return time series.

My original return series (n = 4000) exhibits significant serial autocorrelation at lag 1 & 2, is non-normally distributed (according to Kolmogorov-Smirnoff's test for normality) and exhibits positive excess kurtosis & skewness. Typical properties of financial time series data.

In order to simulate an artifical return time series which exhibits the same statistical properties as my original return series, the parametric residual boostrap is used. This is, the estimated model residuals are resampled with replacement with equal propability. The scrambled residual series is then used in conjunction with the estimated model coeffcients to compute a new artifcial return series (see Chandrashekar, 2005).

According to different papers & textbooks, the residual bootstrap requires the residuals to be i.i.d. $N(0,\sigma^2)$.

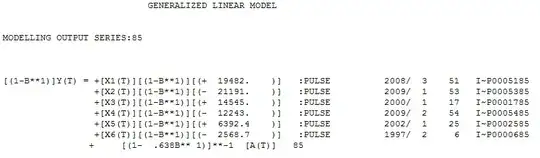
I tested different GARCH specifications. The EGARCH with student-t innovation performed best according to BIC/SIC,Ljung Box and McLeod-Li tests (see output). This is, the standardized residuals are not serially autocorrelated and not heteroscedastic.

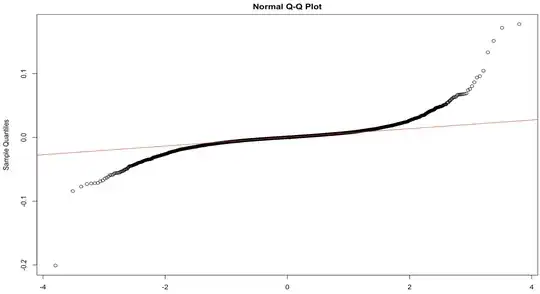
However, when plotting my residuals gaussian normality is not met.

Question 1: Is it a problem to conduct a residual bootstrap if residuals are not gaussian normally distributed?

Question 2: However, Pearson's asjusted Goodness-of-Fit says, that the the empirical distribution of the standardized residuals correspond to the theoretical one from the chosen density (here student t distribution).. Does that mean that the innovations are correclty specified? Is this result implicating a good model. Hence, i should use this model?

enter image description here enter image description here enter image description here enter image description here

References

  1. Chandrashekar, Satyajit. "Simple technical trading strategies: Returns, risk and size." (2005). SSRN.
  2. Marshall, Ben R., Rochester H. Cahan, and Jared M. Cahan. "Does intraday technical analysis in the US equity market have value?." Journal of Empirical Finance 15.2 (2008): 199-210.
Richard Hardy
  • 54,375
  • 10
  • 95
  • 219
lilo
  • 33
  • 5

4 Answers4

1

In a GARCH model, you can assume any of a number of different distributions, not only normal. Actually, one of the stylized facts of financial returns is that the standardized innovations are nonnormal. You need the empirical distribution of standardized innovations to match the assumed distribution. If the assumed distribution is Student-t, you want your empirical distribution to be close to that, not to normal. I would use the model you have and not worry about the fact that standardized innovations are nonnormal.

Regarding

According to different papers & textbooks, the residual bootstrap requires the residuals to be i.i.d. $N(0,\sigma^2)$

I would like to see their explanation for why they need normality. After all, one of the resons bootstrap is so useful is that you do not need to assume a specific parametric distribution for it to work well.

Richard Hardy
  • 54,375
  • 10
  • 95
  • 219
  • Could you give me a reference where it says that you dont need to assume a specific parametric distirbution for the residuals to be resampled in order to generated new artifical returns? – lilo Mar 28 '19 at 18:53
  • I cannot as I do not recall the paper that that proposed bootstrap for GARCH models. However, if you find it, I am quite sure you would not find a requirement for a specific parametric distribution there. – Richard Hardy Mar 28 '19 at 21:17
0

You may have to adjust the df parameter of your student-t distribution. You can fit a student-t distribution in R using the MASS package with fitdistr(). But make sure to check the discussion about Fitting t-distribution in R: scaling parameter. It could also be possible that you have to fit the conditional returns of your GARCH time series to the student-t rather than the raw time series to find the correct df parameter, but I am note sure on that.

sdittmar
  • 206
  • 1
  • 9
0

Please check this paper: https://papers.ssrn.com/sol3/papers.cfm?abstract_id=1611229 and also this one: https://globalriskinstitute.org/publications/systemic-risk-measures-portfolio-choice/

Before you do the bootstrap, you need to remove the correlations between standardized residuals, which can be done using Cholesky decomposition of the estimated correlation matrices. I am not familiar with R but I did something similar in Matlab, so if you need demo codes just message me :).

Joe Lin
  • 3
  • 2
0

There is a whole discussion about using bootstrap in time series data. In dynamic models like GARCH you associate today's volatility with yesterday's and so on. When you sample with replacement the ordering collapses and you usually end up with data having roughly the same moments with the original but different dynamic characteristics. In time series analysis one is advised to use a different technique called block-bootstrap ( https://nccur.lib.nccu.edu.tw/bitstream/140.119/35143/6/51007106.pdf ). In very plain terms you divide your data in blocks (optimal block size is also debated) and you sample those blocks with replacement, just as in the simple bootstrap case. In this way most of the ordering is reserved and thus the simulated series retain the majority of the characteristics of the original data.

Manthos
  • 11
  • 1