61

The title of the Comment in Nature Scientists rise up against statistical significance begins with:

Valentin Amrhein, Sander Greenland, Blake McShane and more than 800 signatories call for an end to hyped claims and the dismissal of possibly crucial effects.

and later contains statements like:

Again, we are not advocating a ban on P values, confidence intervals or other statistical measures — only that we should not treat them categorically. This includes dichotomization as statistically significant or not, as well as categorization based on other statistical measures such as Bayes factors.

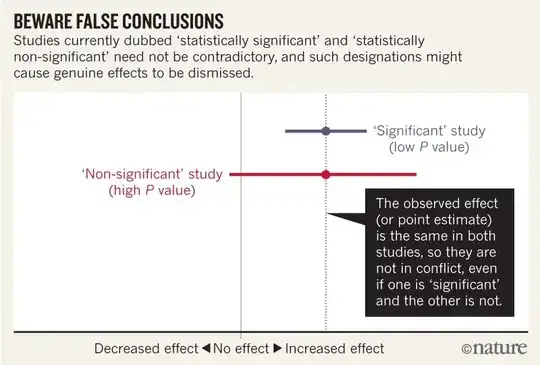
I think I can grasp that the image below does not say that the two studies disagree because one "rules out" no effect while the other does not. But the article seems to go into much more depth than I can understand.

Towards the end there seems to be a summary in four points. Is it possible to summarize these in even simpler terms for those of us who read statistics rather than write it?

When talking about compatibility intervals, bear in mind four things.

  • First, just because the interval gives the values most compatible with the data, given the assumptions, it doesn’t mean values outside it are incompatible; they are just less compatible...

  • Second, not all values inside are equally compatible with the data, given the assumptions...

  • Third, like the 0.05 threshold from which it came, the default 95% used to compute intervals is itself an arbitrary convention...

  • Last, and most important of all, be humble: compatibility assessments hinge on the correctness of the statistical assumptions used to compute the interval...

Nature: Scientists rise up against statistical significance

Community
  • 1
uhoh
  • 685
  • 1
  • 6
  • 10
  • 14
    Basically, they want to fill research papers with even more false positives! – David Mar 21 '19 at 07:23
  • 13
    See the discussion on Gelman's blog: https://statmodeling.stat.columbia.edu/2019/03/20/retire-statistical-significance-the-discussion/. Obviously the article raises some valid points, but see comments raised by Ioannidis _against_ this article (and also, separately, against the "petition" aspect of it), as quoted by Gelman. – amoeba Mar 21 '19 at 08:52
  • 3
    This isn't a new concept though. Meta-analysis has been a thing for the better part of 50 years, and Cochrane have been doing meta-analyses of medical/healthcare studies (where it's easier to standardise objectives and outcomes) for the last 25 years. – Graham Mar 21 '19 at 15:11
  • 6
    Fundamentally the problem is trying to reduce "uncertainty" which is a multidimensional problem to a single number. – MaxW Mar 22 '19 at 19:06
  • 4
    Basically if people stated "we found no evidence of an association between X and Y" instead of "X and Y are not related" when finding $p>\alpha$ this article wouldn't likely exist. – Firebug Mar 22 '19 at 19:35
  • This reminds me of something that I heard in a project managers class. "A fool with a tool is still a fool." – MaxW Mar 23 '19 at 09:40
  • 3
    I get that they are want to not limit beliefs/probabilities to yes/no, but I am just stumped that they spent time decrying hypothesis tests *for difference* in terms on not providing evidence of absence of an effect, while *not* pointing out that this kind of confirmation bias is elegantly eliminated by combining inferences from tests for difference with inference from tests *for equivalence*. Relevance tests are a simple way to place statistical power and effect size directly into the conclusions one draws from a test, while looking at evidence for an effect, and evidence of no effect. – Alexis Mar 23 '19 at 21:17

10 Answers10

67

The first three points, as far as I can tell, are a variation on a single argument.

Scientists often treat uncertainty measurements ($12 \pm 1 $, for instance) as probability distributions that look like this:

uniform probability distribution

When actually, they are much more likely to look like this: enter image description here

As a former chemist, I can confirm that many scientists with non-mathematical backgrounds (primarily non-physical chemists and biologists) don't really understand how uncertainty (or error, as they call it) is supposed to work. They recall a time in undergrad physics where they maybe had to use them, possibly even having to calculate a compound error through several different measurements, but they never really understood them. I too was guilty of this, and assumed all measurements had to come within the $\pm$ interval. Only recently (and outside academia), did I find out that error measurements usually refer to a certain standard deviation, not an absolute limit.

So to break down the numbered points in the article:

  1. Measurements outside the CI still have a chance of happening, because the real (likely gaussian) probability is non-zero there (or anywhere for that matter, although they become vanishingly small when you get far out). If the values after the $\pm$ do indeed represent one s.d., then there is still a 32% chance of a data point falling outside of them.

  2. The distribution is not uniform (flat topped, as in the first graph), it is peaked. You are more likely to get a value in the middle than you are at the edges. It's like rolling a bunch of dice, rather than a single die.

  3. 95% is an arbitrary cutoff, and coincides almost exactly with two standard deviations.

  4. This point is more of a comment on academic honesty in general. A realisation I had during my PhD is that science isn't some abstract force, it is the cumulative efforts of people attempting to do science. These are people who are trying to discover new things about the universe, but at the same time are also trying to keep their kids fed and keep their jobs, which unfortunately in modern times means some form of publish or perish is at play. In reality, scientists depend on discoveries that are both true and interesting, because uninteresting results don't result in publications.

Arbitrary thresholds such as $p < 0.05$ can often be self-perpetuating, especially among those who don't fully understand statistics and just need a pass/fail stamp on their results. As such, people do sometimes half-jokingly talk about 'running the test again until you get $p < 0.05$'. It can be very tempting, especially if a Ph.D/grant/employment is riding on the outcome, for these marginal results to be, jiggled around until the desired $p = 0.0498$ shows up in the analysis.

Such practices can be detrimental to the science as a whole, especially if it is done widely, all in the pursuit of a number which is in the eyes of nature, meaningless. This part in effect is exhorting scientists to be honest about their data and work, even when that honesty is to their detriment.

Ingolifs
  • 1,495
  • 8
  • 28
  • 26
    +1 for *"... publish or perish is at play. In reality, scientists depend on discoveries that are both true and interesting, because uninteresting results don't result in publications."* There was an interesting paper that came out years back that talks about how this "publish or perish" leads to compounding error/bias throughout academia: [Why Most Published Research Findings Are False](https://journals.plos.org/plosmedicine/article?id=10.1371/journal.pmed.0020124) (Ioannidis, 2005) – J. Taylor Mar 21 '19 at 08:03
  • 4
    I don't agree with “the real (likely Gaussian) uncertainty...” – Gaussian is another oversimplification. It's somewhat more justified than the hard-limits model thanks to the Central Limit Theorem, but the _real_ distribution is generally something different still. – leftaroundabout Mar 21 '19 at 08:43
  • @Ingolifs that plot is in R? use `type="s"` or `"S"`. – Hong Ooi Mar 21 '19 at 09:27
  • +1 for the visualization of the imagined distribution. @leftaroundabout yes, though that simplification is acceptable for the most cases. When it isn't, the precision likely is not very high anyway. – Chieron Mar 21 '19 at 09:29
  • 1
    @leftaroundabout The real distribution is likely different still, but unless the value is physically impossible, the probability is likely still mathematically nonzero. – gerrit Mar 21 '19 at 09:38
  • 3
    @leftaroundabout saying that the uncertainty is *likely* Gaussian is not inherently a simplification. It describes a prior distribution, which is justified by the CLT as the best prior in the absence of other supporting data, but by expressing uncertainty over the distribution the acknowledgement that the distribution could well not be Gaussian is already there. – Will Mar 21 '19 at 10:42
  • I miss Mendel.. – Failed Scientist Mar 21 '19 at 14:23
  • 1
    No scientist worth their salt thinks that experimental measurements have zero tails, i.e., are like uniform distribution with absolutely sharp edges – innisfree Mar 22 '19 at 04:43
  • 7
    @inisfree you are very, very mistaken. Many scientific disciplines (like chemistry and biology, as I stated earlier) use almost zero maths, beside basic arithmetic. There are otherwise brilliant scientists out there who are almost math illiterate, and I've met a few of them. – Ingolifs Mar 22 '19 at 06:58
  • @Ingolifs This is surely very field-specific - it's a mistake to be so general and group everyone together by saying that "**Scientists** often treat...". It seems to me that the cases where a professional scientist doesn't need even such basic statistics knowledge are very extreme cases. – aquirdturtle Mar 23 '19 at 01:03
  • 1
    @aquirdturtle definitely not extreme cases. My training was in organic chemistry, which is a pretty large sub-field in and of itself. The intellectual process in organic chemistry is akin to detective work, solving endless crossword puzzles with ambiguous clues, or a giant version of those [word ladder things](https://en.wikipedia.org/wiki/Word_ladder). Higher mathematics is not used, as chemistry is often too complicated for it to come to an answer in a time quicker than just doing the experiment. Many organic chemists will turn pale at the sight of basic algebra, let alone a $\sum$ symbol. – Ingolifs Mar 24 '19 at 09:02
  • 1
    The point I wanted to make is that science is readily performed without maths in many fields outside physics. Nothing about the basic process of scientific inquiry requires that any maths be used. Maths is often only employed when mental models based on 'intuition' and memory start to fail. The statistical work that comes with a particularly thorny question is often only a small part of a non-physicist's research, and this I think is where the problems outlined in the Nature article come from. – Ingolifs Mar 24 '19 at 09:26
  • 1
    One dirty secret of organic chemists is that often they don't even use uncertainty measurements. They'll just state a raw value. 78% yield of final product. There's an unstated understanding that this is inaccurate, but how inaccurate nobody will be able to tell you for a variety of reasons. If you do see a $\pm$, it's because they took the measurement three times, and the quoted uncertainty is half the range. *This is not to say that organic chemists are sloppy*. Very much the opposite, especially when it comes to new compounds. Just that mathematical accuracy isn't terribly important. – Ingolifs Mar 24 '19 at 09:38
  • "_publish or perish is at play._" A better solution IMO would be to increase funding for science at all levels in the process (Ph.D. onward) to be above starvation (or at least precarity) wages, IMO. – ijoseph Mar 27 '19 at 22:47
  • 1
    Thank you for your answer and explanation, this is what I needed. – uhoh Mar 27 '19 at 22:53
20

I'll try.

  1. The confidence interval (which they rename compatibility interval) shows the values of the parameter that are most compatible with the data. But that doesn't mean the values outside the interval are absolutely incompatible with the data.
  2. Values near the middle of the confidence (compatibility) interval are more compatible with the data than values near the ends of the interval.
  3. 95% is just a convention. You can compute 90% or 99% or any% intervals.
  4. The confidence/compatibility intervals are only helpful if the experiment was done properly, if the analysis was done according to a preset plan, and the data conform with the assumption of the analysis methods. If you've got bad data analyzed badly, the compatibility interval is not meaningful or helpful.
ttnphns
  • 51,648
  • 40
  • 253
  • 462
Harvey Motulsky
  • 14,903
  • 11
  • 51
  • 98
20

Much of the article and the figure you include make a very simple point:

Lack of evidence for an effect is not evidence that it does not exist.

For example,

"In our study, mice given cyanide did not die at statistically-significantly higher rates" is not evidence for the claim "cyanide has no effect on mouse deaths".

Suppose we give two mice a dose of cyanide and one of them dies. In the control group of two mice, neither dies. Since the sample size was so small, this result is not statistically significant ($p > 0.05$). So this experiment does not show a statistically significant effect of cyanide on mouse lifespan. Should we conclude that cyanide has no effect on mice? Obviously not.

But this is the mistake the authors claim scientists routinely make.

For example in your figure, the red line could arise from a study on very few mice, while the blue line could arise from the exact same study, but on many mice.

The authors suggest that, instead of using effect sizes and p-values, scientists instead describe the range of possibilities that are more or less compatible with their findings. In our two-mouse experiment, we would have to write that our findings are both compatible with cyanide being very poisonous, and with it not being poisonous at all. In a 100-mouse experiment, we might find a confidence interval range of $[60\%,70\%]$ fatality with a point estimate of $65\%$. Then we should write that our results would be most compatible with an assumption that this dose kills 65% of mice, but our results would also be somewhat compatible with percentages as low as 60 or high as 70, and that our results would be less compatible with a truth outside that range. (We should also describe what statistical assumptions we make to compute these numbers.)

usul
  • 532
  • 2
  • 5
  • 4
    I disagree with the blanket statement that "absence of evidence is not evidence of absence". Power calculations allow you determine the likelihood of deeming an effect of a particular size significant, given a particular sample size. Large effect sizes require less data to deem them significantly different from zero, while small effects require a larger sample size. If your study is properly powered, and you are still not seeing significant effects, then you can reasonably conclude that the effect does not exist. If you have sufficient data, non-significance can indeed indicate no effect. – Nuclear Hoagie Mar 21 '19 at 13:23
  • 1
    @NuclearWang True, but only if the power analysis is done ahead of time and only if it is done with correct assumptions and then correct interpretations (i.e., your power is only relevant to the *magnitude of the effect size* that you predict; "80% power" does not mean you have 80% probability to correctly detect *zero* effect). Additionally, in my experience the use of "non-significant" to mean "no effect" is often applied to *secondary* outcomes or rare events, which the study is (appropriately) not powered for anyways. Finally, beta is typically >> alpha. – Bryan Krause Mar 21 '19 at 15:05
  • 9
    @NuclearWang, I don't think anyone is arguing "absence of evidence is NEVER evidence of absence", I think they are arguing it should not be automatically interpreted as such, and that this is the mistake they see people making. – usul Mar 21 '19 at 17:28
  • It's almost like people are not trained in [tests for equivalence](https://stats.stackexchange.com/tags/tost/info) or something. – Alexis Mar 23 '19 at 21:44
10

The great XKCD did this cartoon a while ago, illustrating the problem. If results with $P\gt0.05$ are simplistically treated as proving a hypothesis - and all too often they are - then 1 in 20 hypotheses so proven will actually be false. Similarly, if $P\lt0.05$ is taken as disproving a hypotheses then 1 in 20 true hypotheses will be wrongly rejected. P-values don't tell you whether a hypothesis is true or false, they tell you whether a hypothesis is probably true or false. It seems the referenced article is kicking back against the all-too-common naïve interpretation.

whuber
  • 281,159
  • 54
  • 637
  • 1,101
digitig
  • 233
  • 1
  • 2
  • 8
    (-1) P-values don't show you whether a hypothesis is **probably** true or false. You need a prior distribution for that. See [this xkcd](https://xkcd.com/1132/), for example. The problematic hand-waving that leads to this confusion is that *if* we have similar priors for a large number of hypothesis, then the p-value will be *proportional* to probability it is true or false. But before seeing any data, some hypothesis are much more probable than others! – Cliff AB Mar 21 '19 at 17:54
  • 3
    While this effect is something that shouldn't be discounted, it is far from being a significant point of the referenced article. – R.M. Mar 21 '19 at 18:10
7

tl;dr- It's fundamentally impossible to prove that things are unrelated; statistics can only be used to show when things are related. Despite this well-established fact, people frequently misinterpret a lack of statistical significance to imply a lack of relationship.

A good encryption method should generate a ciphertext that, as far as an attacker can tell, doesn't bare any statistical relationship to the protected message. Because if an attacker can determine some sort of relationship, then they can get information about your protected messages by just looking at the ciphertexts – which is a Bad ThingTM.

However, the ciphertext and its corresponding plaintext 100% determine each other. So even if the world's very best mathematicians can't find any significant relationship no matter how hard they try, we still obviously know that the relationship isn't just there, but that it's completely and fully deterministic. This determinism can exist even when we know that it's impossible to find a relationship.

Despite this, we still get people who'll do stuff like:

  1. Pick some relationship they want to "disprove".

  2. Do some study on it that's inadequate to detect the alleged relationship.

  3. Report the lack of a statistically significant relationship.

  4. Twist this into a lack of relationship.

This leads to all sorts of "scientific studies" that the media will (falsely) report as disproving the existence of some relationship.

If you want to design your own study around this, there're a bunch of ways you can do it:

  1. Lazy research:
    The easiest way, by far, is to just be incredibly lazy about it. It's just like from that figure linked in the question:
    $\hspace{50px}$.
    You can easily get that $`` {\small{\color{darkred}{\begin{array}{c} \text{'Non-significant' study} \\[-10px] \left(\text{high}~P~\text{value}\right) \end{array}}}} "$ by simply having small sample sizes, allowing a lot of noise, and other various lazy things. In fact, if you're so lazy as to not collect any data, then you're already done!

  2. Lazy analysis:
    For some silly reason, some people think a Pearson correlation coefficient of $0$ means "no correlation". Which is true, in a very limited sense. But, here're a few cases to observe:
    $\hspace{50px}$.
    This is, there may not be a "linear" relationship, but obviously there can be a more complex one. And it doesn't need to be "encryption"-level complex, but rather "it's actually just a bit of a squiggly line" or "there're two correlations" or whatever.

  3. Lazy answering:
    In the spirit of the above, I'm going to stop here. To, ya know, be lazy!

But, seriously, the article sums it up well in:

Let’s be clear about what must stop: we should never conclude there is ‘no difference’ or ‘no association’ just because a P value is larger than a threshold such as 0.05 or, equivalently, because a confidence interval includes zero.

Nat
  • 775
  • 1
  • 5
  • 11
  • +1 cause what you write is both true and thought provoking. However, in my humble opinion, you *can* prove that two quantities are reasonably uncorrelated under certain assumptions. You have to offcourse first start by e.g. supposing a certain distribution about them, but this can be based on the laws of physics, or statistics (e.g. the speed of molecules of a gas in a container are expected to be gaussian or so on) – ntg Mar 22 '19 at 05:21
  • 3
    @ntg Yeah, it's hard to know how to word some of this stuff, so I left a lot out. I mean, the general truth is that we can't disprove that _some_ relationship exists, though we can generally demonstrate that a specific relationship doesn't exist. Sorta like, we can't establish that two data series are unrelated, but we can establish that they don't appear to be reliably related by a simple linear function. – Nat Mar 22 '19 at 08:05
  • This may not be so important for a statistics site, but FYI, most modern encryption schemes do *not* have the property that "the ciphertext and its corresponding plaintext 100% determine each other". Rather, the encryption process usually incorporates additional random padding; if you encrypt the same message multiple times, you'll get different results each time. (The only exceptions I'm aware of are schemes that aim to have the ciphertext be exactly the same length as the plaintext, e.g. for API compatibility reasons, and are willing to sacrifice a bit of security for that.) – ruakh Mar 22 '19 at 23:38
  • @ruakh While I appreciate what you're trying to say, in the above, I was referring to the encryption/decryption transforms. I mean, you're right -- we do all sorts of stuff, like add/remove padding, compress/decompress messages, prepend/remove a nonce, add/check a message's signature with HMAC, add meta-data like a datestamp, etc.. But in the above, I'm specifically talking about the part of crypto that acts on the prepared message to produce the ciphertext and vice-versa, rather than any of the other steps that tend to come before and after that. – Nat Mar 23 '19 at 01:55
  • 1
    -1 "tl;dr- It's fundamentally impossible to prove that things are unrelated": [Equivalence tests](https://stats.stackexchange.com/tags/tost/info) provide evidence of absence of an effect within an arbitrary effect size. – Alexis Mar 23 '19 at 21:46
  • 2
    @Alexis I think you misunderstand equivalence testing; you can use equivalence testing to evidence the absence of a certain relationship holding, e.g. a linear relationship, but not evidence the absence of any relationship. – Nat Mar 24 '19 at 05:21
  • @Nat You are conflating *statistical evidence* with *causal model*. In the world of statistical inference you can provide *as much evidence of **absence of an effect** larger than a specific effect size* as you can provide *evidence of an effect of a specific effect size*. Of *course* there are *causal* biases (predicted on specific kinds of relationships) that can moot *statistical* inferences, but the former apply equally to *evidence of effect* and *evidence of absence of effect*. I agree with your tl;dr only in as much as statistics and science *never **prove***: they only give evidence. – Alexis Mar 24 '19 at 05:32
  • 1
    @Alexis Statistical inference can provide you as much evidence of the absence of an effect larger than a specific effect size _within the context of some model_. Perhaps you're assuming that the model will always be known? – Nat Mar 24 '19 at 05:44
  • I am absolutely not making that assumption. You are simply falsely asserting that lack of knowing the true model prevents statistical evidence of equivalence, but somehow does not prevent statistical evidence of difference. If statistics can provide evidence, it can do so for both presence of an effect and absence of an effect larger than a given effect size – Alexis Mar 24 '19 at 06:16
  • @Alexis So you're claiming to have a universal [distinguishing algorithm](https://en.wikipedia.org/wiki/Distinguishing_attack)? – Nat Mar 24 '19 at 06:22
  • I claim nothing of the sort. However you are privileging statistical evidence of difference over evidence of equivalence. That is *prima facie* [confirmation bias](https://en.wikipedia.org/wiki/Confirmation_bias), hence my downvote. – Alexis Mar 24 '19 at 07:09
  • @Alexis I've been trying to think of a good way to communicate the issue, so if you'd indulge me, I'd like to try here. So I guess my first try is this: If you can detect effects up to a certain size without a model, then how do you define "_size_" without a [measure](https://en.wikipedia.org/wiki/Measure_(mathematics))? – Nat Mar 29 '19 at 01:40
  • @Alexis My second attempt is: Say that I generate a set of data, $f(x),$ as a function of inputs $x \in \left[0, 10\right].$ I'll further guarantee that there's an isometric reverse-mapping, $f^{-1}(x) ,$ such that $x=f^{-1}(f(x)).$ Then, could you use equivalence testing to identify that $x$ and the generated data set are related by a function $f(x) ?$ If so, then that'd be a universal distinguishing algorithm (and be more than worthy of a Fields Medal). If not, then how can you argue that equivalence testing can test for the presence of _any_ relationship? – Nat Mar 29 '19 at 01:47
  • @Alexis My third attempt is: Any two data sets, say $x_1$ and $x_2 ,$ are necessarily describable as being related by an infinity of functions, e.g. high-period sine functions and piecewise functions, such that we're always able to identify infinitely many functions that relate any two data series. If you don't constrain your focus to some specific model, then how can you ever say that _any_ two data series aren't related? (Note that, even if you attempt to use validation, the appended data series will still be related by an infinitely large subset of the original infinite set.) – Nat Mar 29 '19 at 01:54
  • I can update the above answer if we can find something that makes sense. I mean, I can appreciate how someone might hear about equivalence testing and think that it can generally detect for the presence-or-absence of a relationship. So, it'd be nice to expand the above answer with an explanation of why equivalence testing can't be used for that purpose, as I can imagine it being a common misunderstanding. – Nat Mar 29 '19 at 02:01
  • Nat, I teach nonlinear and nonparametric regression to my grad students, and have some of them read the Nature article by Reshef which uses figures bearing a striking similarity to the uncited Wikimedia image in your answer. So I truly appreciate the issue of infinite possible functional relationships for a continuous IV. That is a separate issue from the one I am raising, which I believe is strongly implied in my second comment in that function form is part of a well-specified causal model. Causal inference $\ne$ statistical inference. – Alexis Mar 29 '19 at 15:23
  • Name your statistical model: you can **and should** look combine evidence for equivalence with evidence for difference. – Alexis Mar 29 '19 at 15:30
  • @Alexis Thanks for bearing with me on this. Okay, so, given that we agree that there're an infinity of relationships that can relate any two data series, it's my general position that it's not fruitful to focus on broadly declaring any two data series to be "_unrelated_", since such a statement would require finding the non-significance of infinitely many correlations that could exist between them. Instead, I see statistics as a constructive tool, where we must focus on finding correlations that tend to work. [...] – Nat Mar 30 '19 at 07:20
  • @Alexis As for equivalence testing, I appreciate that it's possible due to a limited number of models. This is, while we can't walk over the general space of all potentially interesting correlations, we _can_ walk over the space of, say, linear correlations. We can then say that the relatively likelihood of a subspace is greater than some threshold of significance, which we can then use as a basis for arguing that the parameters that describe that subspace are valid. Then, for example, we can say that in a linear correlation, the slope is $0 .$ [...] – Nat Mar 30 '19 at 07:25
  • @Alexis For example, I'll agree that we can establish that, within the context of a linear correlation between $x$ and $y ,$ knowledge of $x$ can't be used to inform predictions of a corresponding $y ,$ which one might then describe as there not being a relationship between the two - which, I assume, is what you mean by using equivalence testing. However, my point's that such an observation would be limited to the scope of the model used to perform the equivalence testing, e.g. the linear correlation; that this can't be used to broadly preclude any potentially interesting correlation. – Nat Mar 30 '19 at 07:28
  • @Alexis The relevance to the article being that, in science, we're not typically interested in establishing effects only within a limited subset, but rather we're greedily searching for any sort of effect that we can describe. For example, one study may fail to find a correlation between income and GPA in one context, but this doesn't generally establish that no such correlation that we might appreciate exists, merely that the specific correlations tested for within the experimental context failed to identify such a correlation. The concern being that claims of unrelatedness don't follow. – Nat Mar 30 '19 at 07:35
  • @Alexis Then I think that this is where we'd disagreed earlier - and, I'm hoping, due to ambiguity in communication. This is, I don't believe that equivalence testing can be used in conjunction with a study between GPA and income to broadly establish that the two are unrelated, or that knowledge of a student's GPA can't be used to inform predictions of their later income -- rather, I see equivalence testing as only being able to make such claims within the context of some specific model, which I don't find to be a generally interesting exercise. Would you agree/disagree? – Nat Mar 30 '19 at 07:37
  • Well, no, because inference also happens without models (e.g., dichotomous outcomes in randomized control trials), and equivalence tests are also apt there. But sure I will bite, and **this is my last comment in this thread**: statistical inference is only done in the context of specific models (or designs sans models), and the *moment* you look for statistical evidence of effect in such a model or circumstance, the moment you commit to a statistical relationship you can and should look for evidence of effect, and evidence of no effect. Period. – Alexis Mar 30 '19 at 15:45
4

For a didactic introduction to the problem, Alex Reinhart wrote a book fully available online and edited at No Starch Press (with more content): https://www.statisticsdonewrong.com

It explains the root of the problem without sophisticated maths and has specific chapters with examples from simulated data set:

https://www.statisticsdonewrong.com/p-value.html

https://www.statisticsdonewrong.com/regression.html

In the second link, a graphical example illustrates the p-value problem. P-value is often used as a single indicator of statistical difference between dataset but is clearly not enough by its own.

Edit for a more detailed answer:

In many cases, studies aim to reproduce a precise type of data, either physical measurements (say the number of particles in an accelerator during a specific experiment) or quantitative indicators (like the number of patients developing specific symptoms during drug tests). In either this situation, many factors can interfere with the measurement process like human error or systems variations (people reacting differently to the same drug). This is the reason experiments are often done hundreds times if possible and drug testing is done, ideally, on cohorts of thousands patients.

The data set is then reduced to its most simple values using statistics: means, standard deviations and so on. The problem in comparing models through their mean is that the measured values are only indicators of the true values, and are also statistically changing depending on the number and precision of the individual measurements. We have ways to give a good guess on which measures are likely to be the same and which are not, but only with a certain certainty. The usual threshold is to say that if we have less than one out of twenty chance to be wrong saying two values are different, we consider them "statistically different" (that's the meaning of $P<0.05$), else we do not conclude.

This leads to the odd conclusions illustrated in Nature's article where two same measures give the same mean values but researchers conclusions differ due to the size of the sample. This, and other trops from statistical vocabulary and habits is becoming more and more important in the sciences. An other side of the problem is that people tend to forget that they use statistical tools and conclude about effect without proper verification of the statistical power of their samples.

For an other illustration, recently social and life sciences are going through a true replication crisis due to the fact that a lot of effects were taken for granted by people who didn't check the proper statistical power of famous studies (while other falsified the data but this is another problem).

G.Clavier
  • 149
  • 4
  • Oh that looks really helpful for the uninitiated or who's initiation has expired decades ago. Thanks! – uhoh Mar 21 '19 at 13:12
  • 3
    While not just a link, this answer has all the salient characteristics of a "[link only answer](https://meta.stackexchange.com/a/8259/305499)". To improve this answer, please incorporate the key points into the answer itself. Ideally, your answer should be useful as an answer even if the content of the links disappears. – R.M. Mar 21 '19 at 18:22
  • 2
    About p-values and the base rate fallacy (mentioned in your link), Veritasium published this video called [the bayesian trap](https://www.youtube.com/watch?v=R13BD8qKeTg). – jjmontes Mar 21 '19 at 20:42
  • 2
    Sorry then, I'll try to improve and develop the answer as soon as possible. My idea was also to provide useful material for the curious reader. – G.Clavier Mar 22 '19 at 16:43
  • 1
    @G.Clavier and the self-described statistics newbie and curious reader appreciates it! – uhoh Mar 22 '19 at 22:17
  • 1
    @uhoh Glad to read it. :) – G.Clavier Mar 23 '19 at 18:27
4

For me, the most important part was:

...[We] urge authors to discuss the point estimate, even when they have a large P value or a wide interval, as well as discussing the limits of that interval.

In other words: Place a higher emphasis on discussing estimates (center and confidence interval), and a lower emphasis on "Null-hypothesis testing".

How does this work in practice? A lot of research boils down to measuring effect sizes, for example "We measured a risk ratio of 1.20, with a 95% C.I. ranging from 0.97 to 1.33". This is a suitable summary of a study. You can immediately see the most probable effect size and the uncertainty of the measurement. Using this summary, you can quickly compare this study to other studies like it, and ideally you can combine all the findings in a weighted average.

Unfortunately, such studies are often summarized as "We did not find a statiscally significant increase of the risk ratio". This is a valid conclusion of the study above. But it is not a suitable summary of the study, because you can't easily compare studies using these kinds of summaries. You don't know which study had the most precise measurement, and you can't intuit what the finding of a meta-study might be. And you don't immediately spot when studies claim "non-significant risk ratio increase" by having confidence intervals that are so large you can hide an elephant in them.

Martin J.H.
  • 161
  • 4
  • That depends on one's null hypothesis. For example, rejecting [$H_{0}:|\theta|\ge \Delta$](https://stats.stackexchange.com/tags/tost/info) provides evidence of an absence of effect larger than an arbitrarily small $\Delta$. – Alexis Mar 23 '19 at 21:48
  • 1
    Yes, but why even bother discussing such a hypothesis? You can just state the measured effect size $\theta\pm\delta\theta$ and then discuss what the best/worst case ramifications are. This is how it is typically done in physics, for example [when measuring the mass-to-charge difference between proton and antiproton](https://www.nature.com/articles/nature14861.pdf). The authors could have chosen to formulate a null hypothesis (maybe, to follow your example, that the absolute difference is greater than some $\Delta$) and proceeded to test it, but there is little added value in such a discussion. – Martin J.H. Mar 30 '19 at 19:58
3

It is a fact that for several reasons, p-values have indeed become a problem.

However, despite their weaknesses, they have important advantages such as simplicity and intuitive theory. Therefore, while overall I agree with the Comment in Nature, I do think that rather than ditching statistical significance completely, a more balanced solution is needed. Here are a few options:

1. "Changing the default P-value threshold for statistical significance from 0.05 to 0.005 for claims of new discoveries". In my view, Benjamin et al addressed very well the most compelling arguments against adopting a higher standard of evidence.

2. Adopting the second-generation p-values. These seem to be a reasonable solution to most of the problems affecting classical p-values. As Blume et al say here, second-generation p-values could help "improve rigor, reproducibility, & transparency in statistical analyses."

3. Redefining p-value as "a quantitative measure of certainty — a “confidence index” — that an observed relationship, or claim, is true." This could help change analysis goal from achieving significance to appropriately estimating this confidence.

Importantly, "results that do not reach the threshold for statistical significance or “confidence” (whatever it is) can still be important and merit publication in leading journals if they address important research questions with rigorous methods."

I think that could help mitigate the obsession with p-values by leading journals, which is behind the misuse of p-values.

Krantz
  • 556
  • 2
  • 18
  • 1
    Thanks for your answer, this is helpful. I'll spend some time reading Blume et al. about *second-generation p-values*, it seems to be quite readable. – uhoh Mar 27 '19 at 22:52
3

It is "significant" that statisticians, not just scientists, are rising up and objecting to the loose use of "significance" and $P$ values. The most recent issue of The American Statistician is devoted entirely to this matter. See especially the lead editorial by Wasserman, Schirm, and Lazar.

Russ Lenth
  • 15,161
  • 20
  • 53
  • 1
    Thank you for the link! It's an eye-opener; I didn't realize there was so much thought and debate about this. – uhoh Mar 27 '19 at 22:46
1

One thing that has not been mentioned is that error or significance are statistical estimates, not actual physical measurements: They depend heavily on the data you have available and how you process it. You can only provide precise value of error and significance if you have measured every possible event. This is usually not the case, far from it!

Therefore, every estimate of error or significance, in this case any given P-value, is by definition inaccurate and should not be trusted to describe the underlying research – let alone phenomena! – accurately. In fact, it should not be trusted to convey anything about results WITHOUT knowledge of what is being represented, how the error was estimated and what was done to quality control the data. For example, one way to reduce estimated error is to remove outliers. If this is removal is also done statistically, then how can you actually know the outliers were real errors instead of unlikely real measurements that should be included in the error? How could the reduced error improve the significance of the results? What about erroneous measurements near the estimates? They improve the error and can impact statistical significance but can lead to wrong conclusions!

For that matter, I do physical modeling and have created models myself where 3-sigma error is completely unphysical. That is, statistically there's around one event in a thousand (well...more often than that, but I digress) that would result in completely ridiculous value. The magnitude of 3 interval error in my field is roughly equivalent of having best possible estimate of 1 cm turning out to be a meter every now and then. However, this is indeed an accepted result when providing statistical +/- interval calculated from physical, empirical data in my field. Sure, narrowness of uncertainty interval is respected, but often the value of best guess estimate is more useful result even when nominal error interval would be larger.

As a side note, I was once personally responsible for one of those one in a thousand outliers. I was in process of calibrating an instrument when an event happened which we were supposed to measure. Alas, that data point would have been exactly one of those 100 fold outliers, so in a sense, they DO happen and are included in the modeling error!

Geenimetsuri
  • 31
  • 2
  • "You can only provide accurate measure, if you have measured every possible event." Hmm. So, accuracy is hopeless? And also irrelevant? Please expand on the difference between accuracy and bias. Are the inaccurate estimates biased or unbiased? If they are unbiased, then aren't they a little bit useful? "For example, one way to reduce error is to remove outliers." Hmm. That will reduce sample variance, but "error"? "...often the value of best guess estimate is more useful result even when nominal error interval would be larger" I don't deny that a good prior is better than a bad experiment. – Peter Leopold Mar 21 '19 at 16:27
  • Modified the text a bit based on your comment. What I meant was that statistical measure of error is always an estimate unless you have all the possible individual tests, so to speak, available. This rarely happens, except when e.g. polling a set number of people (n.b. not as samples from larger crowd or general population). – Geenimetsuri Mar 21 '19 at 17:49
  • 1
    I am a practitioner who uses statistics rather than a statistician. I think a basic problem with p values is that many who are not familiar with what they are confuse them with substantive significance. Thus I have been asked to determine which slopes are important by using p values regardless of whether the slopes are large or not. A similar problem is using them to determine relative impact of variables (which is critical to me, but which gets surprisingly little attention in the regression literature). – user54285 Mar 22 '19 at 23:10