In textbook ordinary least squares we want to find a vector of coefficients $b_{k+1\times n}$ such that the sum of the squared deviations of what's observed ($y_{n\times 1}$) from what's assumed to be systematic $Xb$ (or $u'u$ for $u=y-Xb$) is minimized. In addition to the observables $y,X$ we make assumptions about the distribution of $u$ eg $u\sim N(0,1)$.
Is it possible to solve for the inverse linear problem ie. given observables $X$ and an arbitrary but given $b^*$ vector of coefficients, we wish to derive those $y$ that would have produced as a solution of the direct problem, the exact vector $b^*$?
My Approach
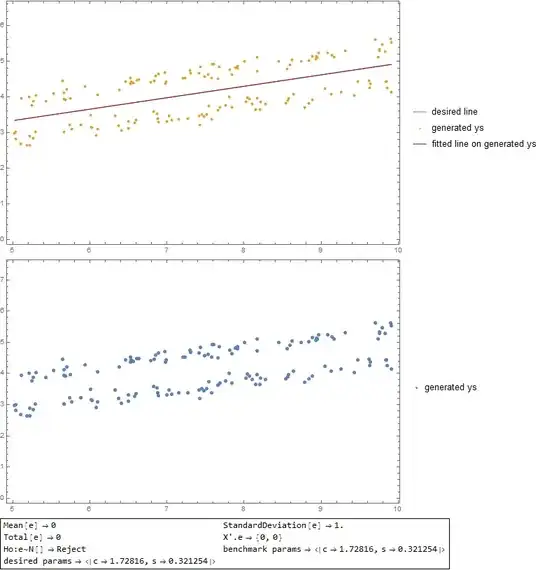
I have tried producing $u$ such that for $g=X'u$, $g'g$ is minimized but the result does not produce reasonably looking $y$'s even though when the $y's$ are used in the direct problem as a dependent variable yields the desired $b^*$'s.
(The generated $y$ data seem to be evenly dispersed above and below the regression line, leaving a narrow corridor around the regression line empty, as illustrated below:
Motivation
The motivation is to be able to generate datasets (collections of $n$ $y$'s) that display persistently the desired regression line (given by the $b^*$'s) when OLS is used on them, for a given set of regressors $X$.