Does the peak of a Normal Distribution mean anything?

Question

What does the peak of a Normal distribution show? Let's say if I have a flat peak, does this mean I have a larger variance? What if I have a sharp peak?

For example,

Does the "blue distribution" have a larger variance?

picture found at "https://www.statisticshowto.datasciencecentral.com/probability-and-statistics/statistics-definitions/kurtosis-leptokurtic-platykurtic/"

According to the text in your link, only the black distribution is normal. The navy blue distribution is not normal, so it's not really clear what you're meaning to ask. Are you asking about the meaning of peaks of *any* distribution? Or are you only concerned with normal distributions? — Sycorax, Mar 08 '19 at 19:36
Related post: https://stats.stackexchange.com/questions/84158/how-is-the-kurtosis-of-a-distribution-related-to-the-geometry-of-the-density-fun — SecretAgentMan, Mar 08 '19 at 20:37
The magenta distribution doesn't even have a "peak" or it may have a measurable set comprising its "peak" depending how you define it. Only one distribution is normal. All but two are log-concave. Their only commonality is that they are symmetric. They are all scale distributions, so can be set to having equal variance. It's perhaps more useful to ask which ones have heavier tails. — AdamO, Mar 08 '19 at 20:55

score 1 · Accepted Answer · answered Mar 08 '19 at 20:34

This answers your question

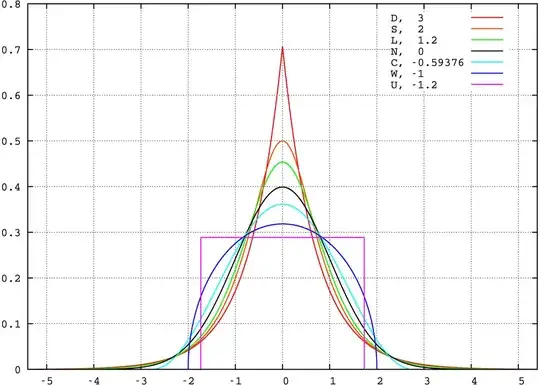
Does the "blue distribution" have a larger variance?

and does not address the broader answer. I recommend this post as a start point.

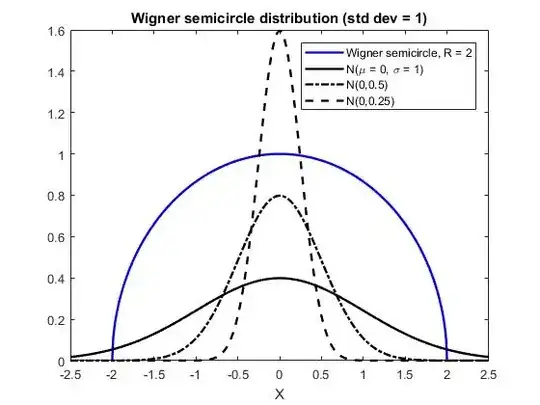
The "blue distribution" is the Wigner semicircle distribution.

In the figure below, $R=2$ which implies that if $X\sim \text{WignerSemicircle}(R)$, then $\text{var}(X) = \frac{R^2}{4}=1$. You can compare that with different Normal (Gaussian) distributions with the same mean but different variances. Note the standard deviation is given in the plot legend.

It appears your "blue distribution" has a larger variance than the "black distribution."

% MATLAB R2017a
R = 2;
fh=@(x) 2*(1./(R^2)).*sqrt((R^2) - (x.^2));

X = -2:.01:2; 
XN = -2.5:.01:2.5;

figure, hold on
plot(X,fh(X),'b-','DisplayName','Wigner semicircle, R = 2')
plot(XN,normpdf(XN,0,1),'k-','DisplayName','N(\mu = 0, \sigma = 1)')
plot(XN,normpdf(XN,0,0.5),'k-.','DisplayName','N(0,0.5)')
plot(XN,normpdf(XN,0,0.25),'k--','DisplayName','N(0,0.25)')
legend('show')

Does the peak of a Normal Distribution mean anything?

1 Answers1