Wikipedia gives several summary statistics for bimodality.
I will give some useful examples:
Sarle's bimodality coefficient
Reminiscent of a proposal by Pearson's, it builds on the idea that bimodal distributions present low kurtosis, high skewness, or both at the same time.
$\gamma$ is the skewness while $\kappa$ is kurtosis.
$\beta \in [0,1]$.
$\beta = 5/9$ for uniform and exponential distributions. Values greater than that indicate bimodality.
$$
\beta = \frac{\gamma^2+1}{\kappa}
$$
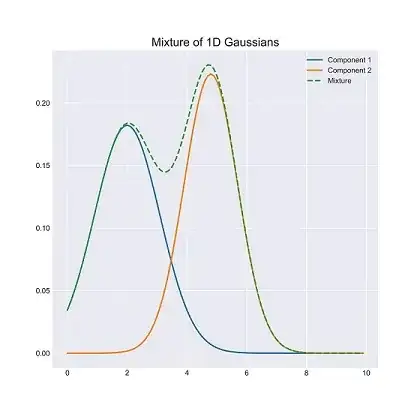
Ashman's D
$D$ measures the degree of separation between two Gaussian components.
$D>2$ is an indicator of marked separation between the distributions.
You can use it if you have the probability distribution function or if you can model your samples with a bimodal Gaussian mixture.
$$D=\sqrt2\frac{|\mu_1-\mu_2|}{\sqrt{\sigma_1^2+\sigma_2^2}}$$
van der Eijk's A
$A$ can be used to summarize bimodality directly from the samples' histogram.
$S$ is the number of categories with non-zero counts, while $K$ is the total number of categories.
$U$ is a binary measure of unimodality, and is only equal to one if there's equidistribution of samples across one or more category.
$A=-1$ suggests bimodality while $A=1$ indicates unimodality.
$$A = U\left(1-\frac{K-1}{S-1}\right)$$