Manually calculate SARIMAX forecast

Question

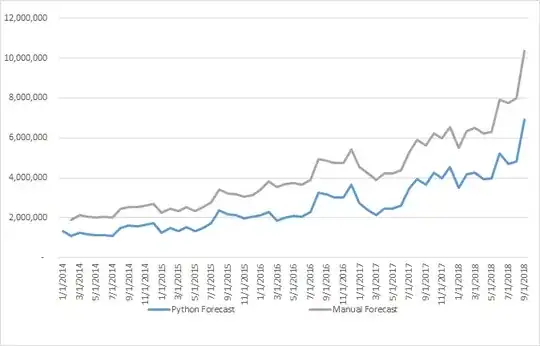
I'm trying to manually replicate the forecast that I obtained using statsmodels.api sarimax (python). Its actually just an AR(1) model with one exogenous variable, in the form of SARIMAX(1,0,0)(0,0,0)12

The results obtained using the statsmodels library are as follows:

The obtained function is y_t = 1088 + 0.6145*y_t-1 + 185500*x (see image above) Nonetheles, when I manually input those values into the function, my results are very different.

I would very much appreciate if someone could give me a hint on what I'm doing wrong regarding the manual calculation.

P.S.:I apologize if the formatting of the question is not up to standards. This is my first post here.

Answer 1

The issue is that the model you are thinking of is an ARMAX model, like:

$$y_t = \mu + \beta x_t + y_{t-1} + \varepsilon_t$$

But Statsmodels fits a regression with ARMA errors. So the model in statmodels is:

$$ y_t = \beta x_t + u_t \\ u_t = \mu + \eta_{t-1} + \zeta_t \\ $$

It looks like you probably did something like the following in Statsmodels:

mod = sm.tsa.SARIMAX(endog, order=(1, 0, 0), trend='c', exog=exg)
res = mod.fit()

To reconstruct the forecast from Statsmodels, you can do the following:

# Compute u_t for in-sample values
ut_insample = endog - (185500 * exog)

# Forecast u_T+h for h = 1, ..., 10
ut_forecast = np.zeros(10 + 1)  # e.g. to forecast 10 periods
ut_forecast[0] = ut_insample[-1]
for t in range(1, len(ut_forecast)):
    ut_forecast[t] = 1088 + 0.6145 * ut_forecast[t-1]
ut_forecast = ut_forecast[1:]

# Get the forecast you want by adding back in the
# effect of the exogenous variables
# Note: this assumes that you have some values `exog_forecast` available
endog_forecast = 185500 * exog_forecast + ut_forecast

Answer 2

Following your answer and the equation explaining regression with ARMA errors: Why do you have different results (coef) of the exogenous variables if you change the order (i.e. p=1 or p=2).

Thank you in advance