I have this table:
The table shows the occurrences for each feature and separates whether one has or not musical knowledge. I'd like to show in the test column a 'number' that could tell how strong a feature is correlated to the fact that one has musical knowledge. Which statistical test would you suggest? I'm probably complicating things too much, but anyways.
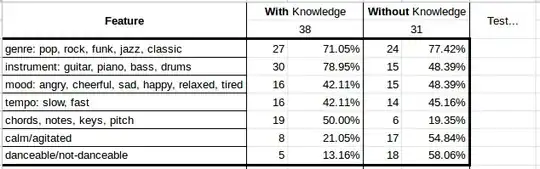
It seems like, for each feature, you really have a contingency table ($2\times 2$ table.) For instance, for the first row, the table is
know genre total
W know 27 38
Wout know 24 31
(please comment if my interpretation is wrong). Usually (for chisquare test and other calculation ) we want a table with rows $(x, n-x)$ not as above $(x,n)$, that is:
genre don't
W know 27 11
Wout know 24 7
If this feature is meaningful, at least we should be able to reject the null of homogeneity. Using the chi-square test gives:
Pearson's Chi-squared test with Yates' continuity correction
data: tab
X-squared = 0.10466, df = 1, p-value = 0.7463
In this case, we could not reject, so this feature is not helpful. Now you can repeat this for all features. In the reject cases, some measure of effect size, like the (log) odds ratio, can be helpful. Or you could bypass the chisquare test and calculate, say, odds ratios with confidence intervals at the outset. Odds ratios could be calculated either directly or via logistic regression, this is discussed widely, see for instance this blog or Computing Confidence Intervals for Odds Ratio Based on Fitted Values. There is even a dedicated package on CRAN. See also Different ways to produce a confidence interval for odds ratio from logistic regression.
If you also have the original data your tables were calculated from, you could try to use logistic regression directly.