0

Setting

Probability theory can be a weird place sometimes. Here I was, confident in my insane math skills, trying to solve the following problem:

Let $N, \alpha$ and $\beta$ be given.

  • Draw $N$ coins from a fixed bag with different coins, such that the success probability for each coin is unknown but modeled by a Beta distribution $Beta(\alpha, \beta)$.
  • Flip each coin from the bag once and count the number of successes.

How are the number of successes distributed?

Realisation of ignorance

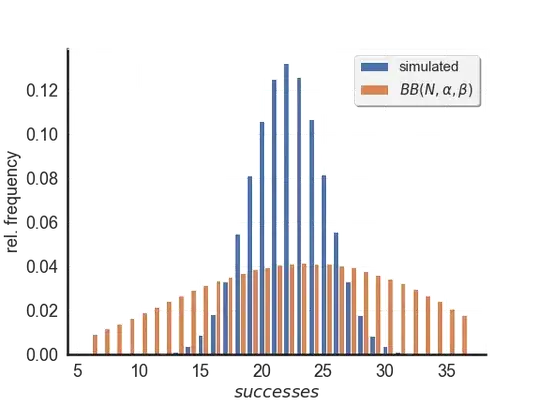
"Pff, what an insult!", I thought. "It's obviously the Beta-Binomial distribution!", my inner Icarus cried. You can simply check that with an easy (Python) implementation:

sample_size = 2**20

N = 42
alpha = 3.14159
beta  = 2.71828

coins = np.random.beta(alpha, beta, size=N)

sample = []
for i in range(sample_size):
    R = np.random.uniform(size=N)
    wins = np.sum(np.where(coins>R, 1, 0))
    sample.append(wins)

Now we can compare mean and variance and that should be enough for the sanity check:

>>> print(np.mean(sample), N*alpha/(alpha+beta))
22.00448989868164 22.517014882582718

Well, that error is tolerable; we're dealing here with probabilities after all. Let's move on to the variance

>>> print(np.var(sample), N*alpha*beta*(alpha+beta+N)/((alpha+beta)**2 * (alpha+beta+1)))
8.996273862416274 72.87400738804808

... EXCUSE ME?!

This can't be true. Lemme draw a histogram:

enter image description here

A desperate attempt

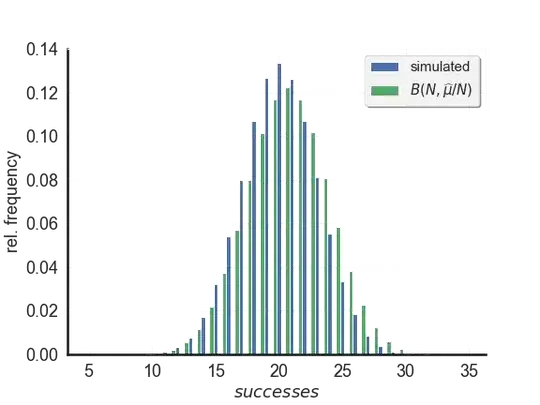
Okay. After sitting down for a while, questioning my existence, I swallow my pride and complied with what I perceived as reality. The simulated experiment kinda looked like a binomial distribution, let's do a quick check:

enter image description here

where $\widehat{\mu}$ is the sample mean. That doesn't look too bad after all, maybe a $\chi^2$-test can formalize our visuals:

>>> cats, f_obs = zip(*[(cat, len(list(group))) for cat,group in groupby(sorted(sample))])
>>> f_exp = scipy.stats.binom.pmf(k=cats, n=N, p=np.mean(sample)/N)*sample_size
>>> 
>>> scipy.stats.chisquare(f_obs=f_obs, f_exp=f_exp)
Power_divergenceResult(statistic=14303.936045316765, pvalue=0.0)

*drops the mic and leaves the room in shame*

Cry for help

At this point I gave up completely on making any further pseudo-educated guesses and started to consult the Interweb for its glorious wisdom. I stumbled upon this answer but @probabilityislogic seems to be suggesting to do exactly what I have done.

Can someone please help me to get some insights for the distribution that results from the above mentioned experiment?

Stephan Kolassa
  • 95,027
  • 13
  • 197
  • 357
chickenNinja123
  • 141
  • 4
  • I figured so far, that the Beta-Binomial distribution is suited for ["the binomial distribution in which the probability of success at each trial is **fixed** but randomly drawn from a beta distribution"](https://en.wikipedia.org/wiki/Beta-binomial_distribution), whereas in my case the coins are drawn newly after each trial and hence results to a different distribution. – chickenNinja123 Feb 22 '19 at 10:20
  • Isn't that a sum of Beta-Binomial variates? – Xi'an Feb 22 '19 at 10:22
  • Hm... you mean it's the sum of independent Beta-Binomial distributions, with $N=1$? That would make sense... – chickenNinja123 Feb 22 '19 at 10:27
  • @Xi'an but isn’t the Beta-Binomial for $n=1$ just a Bernoulli distribution? That would mean that the sum should be binomially distributed... – chickenNinja123 Feb 28 '19 at 19:30

1 Answers1

1

Your error is that you use precisely the same $42$ probabilities (coins) in each of the $2^{20}$ simulations, and so lose the element of sample variance which would come from these varying

You would get the Beta-Binomial distribution if you chose new probabilities each time, for example putting 

coins = np.random.beta(alpha, beta, size=N)

inside the for loop

Henry
  • 30,848
  • 1
  • 63
  • 107
  • Thanks for this insight! I guess my question then is not well posed. In my actual problem where I need this the bag of coins indeed is fixed, and we only know that the success probabilities of the (unknown but fixed) coins are modeled by a Beta-distribution. – chickenNinja123 Feb 22 '19 at 10:45
  • I modified the question box now. – chickenNinja123 Feb 22 '19 at 10:48