2

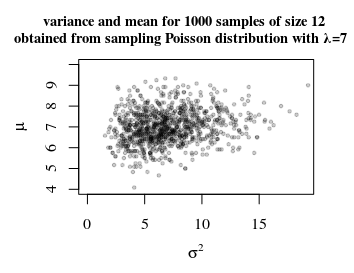
Let's say a city has 7 accidents per 30 days on average.

We can use Poisson distribution formula where $\lambda = 7$

$$\frac 1 {n!} (\lambda t)^n e^{-\lambda t}$$

But in Poisson distribution the lambda equals variance. In this case variance is $12.$ So we can't use Poisson.

But why we can't use Poisson distribution, what does it mean variance is not equal to lambda?

Community
  • 1
Coder88
  • 159
  • 7
  • 2
    perhaps you mean *negative binomial* distribution? It seems to have the characteristics that you mention: support on non-negative integers, variance can be larger than the mean – Sycorax Feb 14 '19 at 20:43
  • @Sycorax I think I need to edit the question. – Coder88 Feb 14 '19 at 21:32
  • 2
    Let me make sure I understand the logic of your question: you want to model data with a particular distribution; that distribution implies the mean and variance should be approximately equal; but that is not the case for your data. Wouldn't this observation naturally be taken as evidence that your model is so wrong as to be useless of misleading? In light of that, what are you trying to ask? – whuber Feb 14 '19 at 21:50
  • @whuber yes Poisson can't be used there, but I don't understand why that is the case, and this is what I'm trying to ask. – Coder88 Feb 14 '19 at 21:54
  • 1
    I am struggling to understand what the difficulty is here. Do you suppose it makes sense to continue to use a model that, as you have pointed out, leads to erroneous conclusions about the data? – whuber Feb 14 '19 at 21:59
  • @whuber. This is not what I suppose. I just wonder how can we show mathematically why variance not being equal to lambda makes Poisson distribution not a suitable model to use? – Coder88 Feb 14 '19 at 22:20
  • 2
    It's a bit like asking why can't I model a shape as a square when it looks rectangular? – seanv507 Feb 14 '19 at 23:17
  • 3
    If you *observe* 7 accidents in 30 days, even if it is from a Poisson process, you *don't* have a Poisson(7) (assuming 30 days is the unit of time); it's a random observation from a Poisson, entirely consistent with a wide range of possible $\lambda$ values. How did you compute this variance of 12? – Glen_b Feb 15 '19 at 01:48
  • Since having a Poisson variate implies that the variance is *always* equal to $\lambda$, if the variance is not equal to $\lambda$, what does that imply about whether the distribution is Poisson? Isn't that mathematical in nature: $A \rightarrow B$, therefore $\sim B \rightarrow \sim A$? – jbowman Feb 15 '19 at 03:54
  • I agree with @Sycorax. When you consider a counting problem in which there is experimental evidence that $var(x) \ne E(x)$, it is natural to assume a mixture of Poissons. The beta-binomial will describe the parameter $\lambda$, and a negative binomial will describe the posterior predictive distribution of the number of counts. – Peter Leopold Feb 15 '19 at 04:32

1 Answers1

2
  • You observe a mean of 7 per day with a variance of 12.
  • You imagine that the process is (should be) a Poisson process.

These two are contradicting since for a Poisson distribution of the data you would expect equal mean and variance.

So one of the two premisses must be false.

  • It could be that the measurements are not correct. Or possibly the data set is only small such that it is incorrect to interpret the values $\mu=7$ and $\sigma^2=12$ as good estimates for the parameters of the distributiuon.

    I see you have a related question on the math.stackexchange where you mention that the data are accidents per month. I can imagine that with this low frequency of sampling you do not have a large data set. Say you only have data of a single year (12 points), and if the data is hypotetically distributed according to a Poisson distribution with $\lambda=7$, then the distribution for the means and variance of your sample would look like the image below:

    1000 samples with 12 iid poisson distributed variables

    So while the mean and variance of the Poisson distribution are be equal, the same is not true for the particular samples that are sampled from a Poisson distribution.

  • It could be (and I believe it is likely) that you do not have a (single) Poisson process. This would namely be the situation that the probability of an accident is constant in time.

    An example how you could have a different situation is when you have the situation that the weekends have a lower rate of accidents (and probably there will be more different types of variations, day/night, winter/summer, peak hours, holidays, etc). In this simple example you get a mixture of two Poisson distributions: $$f(k) = \frac{2}{7} \frac{(\lambda-5a)^k e^{-(\lambda-5a)}}{k!} + \frac{5}{7} \frac{(\lambda+2a)^k e^{-(\lambda+2a)}}{k!}$$ When $\lambda = 7$ and $a=\sqrt{0.5}$, then you have a mean 7 and variance 12. example

Thus a situation with $\lambda_\text{weekdays} \approx 8.41$ and $\lambda_\text{weekend} \approx 3.46$ could explain your observation. But, of course, this is only one of many examples how the probability for accidents is not constant in time and you should investigate this further. If you look for overdispersion you will be able to find hints how to deal with your problem.

Sextus Empiricus
  • 43,080
  • 1
  • 72
  • 161
  • Thanks for the explanation. The data are from CSV file, number of accidents per month, from 20 years. I calculated the mean is ca 7 (average 7 accidents per month), and variance is ca 12. – Coder88 Feb 15 '19 at 14:00
  • 1
    In that case you have the second situation. The mean accidents per month is not a constant. You can expect it to vary throughout the 20 years. However, this does not mean that you can not model this as a Poisson distributed variable. You can have the situation that the *conditional* accidents per month is Poisson distributed (where the parameter $\lambda$ follows some function of time). A related issue is this:https://stats.stackexchange.com/questions/12262 and https://stats.stackexchange.com/questions/342759 – Sextus Empiricus Feb 15 '19 at 15:22