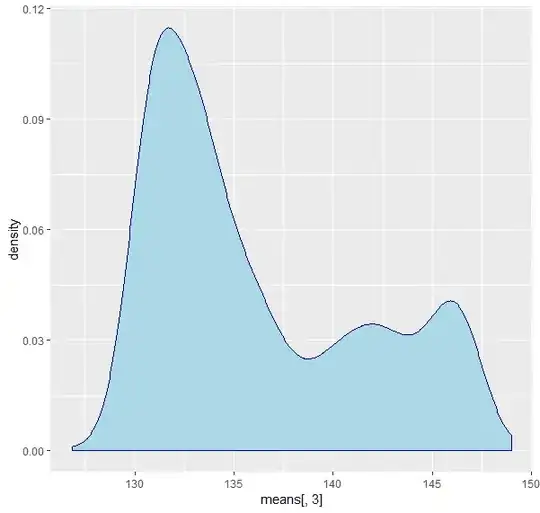
I have tested the central limit theorem with 1000 samples and a sample size of 4. The resulting distribution was nowhere near normal, and when I used n = 30, it did start looking normal.
Is there a theoretical basis for this "rule of thumb"?
The resulting distribution looks like this: