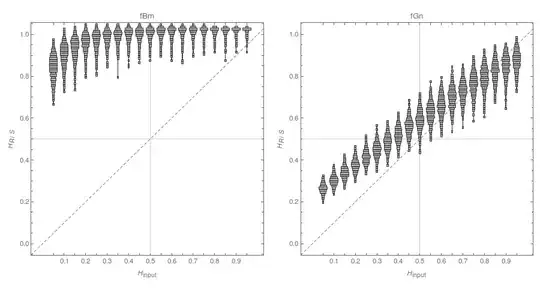
I've used the standard R/S algorithm for estimating the Hurst exponent in Mathematica*, and tested it on fBm and fGn for $H\in\{0.05,0.1,\ldots,0.95\}$, generating 1000 time series for each $H$. The results, in form of violin plots, are as follows:
While for fGn the performance is somewhat ok (although anti-persistent processes are systematically overestimated), I was surprised to see the awful performance in case of fBm. I hadn't found anywhere an indication that R/S is not suitable for nonstationary data, so I always assumed it's a universal algorithm.
After seeing these results, I've done some more digging and only found this paper: Bias in estimating fractal dimension with the rescaled-range (R/S) technique suggesting that $H>1$ is a sign of nonstationarity.
Is this bias (for both fBm and fGn) something well-known that I've just been constantly missing? Has it been thoroughly examined, and is there some study to reference?
I have also generated a few fBm (and fGn through differencing) and estimated their $H$ using R's hurstexp function, finding a similar pattern; so it seems it's a real phenomenon, not a sloppy implementation.
*http://demonstrations.wolfram.com/HurstExponentOfStockPrice/