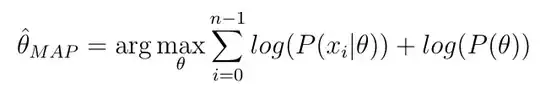With prior $\mathsf{Unif}(0,1) \equiv \mathsf{Beta}(\alpha_0=1,\beta_0 =1)$ and likelihood
$\mathsf{Binom}(n, \theta)$ showing $x$ successes in $n$ trials, the posterior distribution is $\mathsf{Beta}(\alpha_n=1 + x,\; \beta_n = 1 + n - x).$
(This is easily seen by multiplying the kernels of the prior and likelihood to get the kernel of the posterior.)
Then the posterior mean
is $$\mu_n = \frac{\alpha_n}{\alpha_n+\beta} = \frac{x+1}{n+2}.$$
In a Bayesian context, just using the terminology posterior mean may be best. (The median of the posterior distribution and the maximum of its PDF have also been used to summarize posterior information.)
Notes: (1) Here you are using $\mathsf{Beta}(1,1)$ as a noninformative prior distribution. On sound theoretical grounds, some Bayesian statisticians prefer to use
the Jeffreys prior $\mathsf{Beta}(\frac 1 2, \frac 1 2)$ as a noninformative prior. Then the posterior mean is $\mu_n = \frac{x+.5}{n+1}.$
(2) In making frequentist confidence intervals Agresti and Coull have suggested "adding two successes and two failures" to the sample in order to get a confidence interval based on the estimator $\hat p = \frac{x+2}{n+4},$ which has more accurate coverage probabilities (than the traditional Wald interval using $\hat p = \frac x n).$ David Moore has dubbed this a plus-four estimator in some of his widely-used elementary statistics texts, and the terminology has been used by others. I would not be surprised to see your estimator called 'plus two' and Jeffries' called 'plus one'.
(3) All of these estimators have the effect of 'shrinking the estimator towards 1/2' and so they have been called 'shrinkage estimators,' (a term that is much more widely used, particularly in James-Stein inference). See Answer (+1) by @Taylor.