I have some pairs of data ${(x_1,y_1),..., (x_n,y_n)}$ genereated by some process and would like to fit it with a function so that $y_i \approx \hat{f}(x_i)$.
By plotting the $(X,Y)$ on a 2D plot, and eyeballing, we find the relationship of data is monotonically decreasing, and the shape is similar to $y=x^{-\alpha}$ where $0<\alpha<1$.
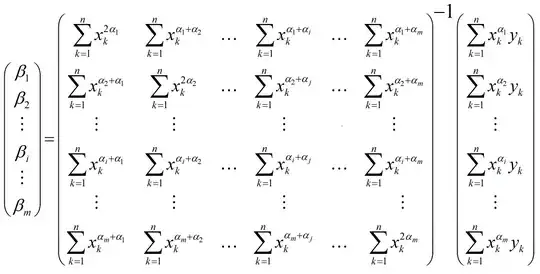
The idea then is to use the sum of a series of basis functions to fit the data. In other words, let $\hat{f}(x)=\sum_{i=1}^m \beta_i h_i(x)$ where $h_i(x)= x^{-\alpha_i}$ for a set of predefined $\alpha$'s - ${\alpha_1, \alpha_2..., \alpha_m}$, where $0<\alpha_i<1$. We can then fit the data and find the $\beta_1,.., \beta_m$ with least squares.
My question is then is if the basis functions $h(x)=x^{-\alpha_i}$ are okay to use? Do I need to somehow make the basis function better? Is there any better ideas?