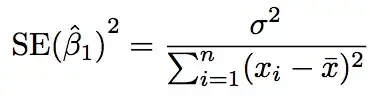I am working with Likelihood to Recommend metric that's measured on a scale of 1-10. The objective is to test for statistically significant improvement/decline (period over period) in the metric. On a side note, the distribution of this metric is heavily skewed towards higher ratings, especially 9-10 (dummy data below may not be reflective of that)
Here is what I have already tried in past:
Aggregate the data to use top-2 boxes (% of 9-10) and run a chi-square test of independence (proportions test).
Aggregate the data to use Net Promoter Score (% of 9-10 minus % of 1-6) and calculate Margin of Error.
Aggregate the data to use Net Promoter Score (% of 9-10 minus % of 1-6) and run a chi-square test to test for difference in the composition of NPS.
Those methods seem to work well but I am curious about the appropriateness of running a Wilcoxon Mann Whitney Rank Sum Test. The data is unpaired and sample sizes are large(>1000). What are your thoughts?